
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Параллельное проецирование
|
|
Частный случай центрального проецирования с центром проекций, находящимся в бесконечности (в несобственной точке O). Осуществляется связкой лучей заданного направления S (рис. 2).
Аппарат параллельного проецирования:
a -- плоскость проекций;
S — направление проецирования;
[ O ¥ A ]½½[ O ¥ B ] ¼½½ S
A a = [ OA ] a — параллельная проекция точки А на плоскость;
l a = b(AA a½½ BB a) I a —параллельная проекция прямой на плоскость a.
Обратимости нет. Одна центральная проекция точки не позволяет судить о положении точки в пространстве. А = D
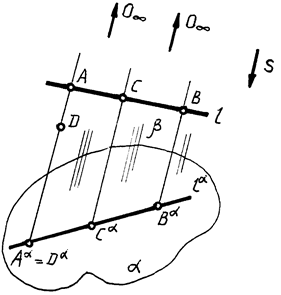 Рис. 2
Рис. 2
|
Инвариантные свойства параллельного проецирования
Геометрические фигуры проецируются на плоскость проекций, в общем случае, с искажением. Характер искажений зависит от аппарата проецирования и положения проецируемой фигуры относительно плоскости проекций.
В частности, при параллельном проецировании нарушаются метрические характеристики геометрических фигур (искажаются линейные и угловые величины). Некоторые свойства фигуры сохраняются на ее проекции.
Сохраняющиеся в проекции свойства фигуры называются независимыми или ИНВАРИАНТНЫМИ. Эти инвариантные свойства часто называют сокращенно: инварианты.
Инварианты параллельного проецирования
1. Проекция точки есть точка (рис. 1; рис.2)
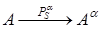
2. Проекция прямой есть прямая (рис. 1; рис.2)
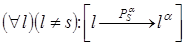 *
*
3. Проекция точки, принадлежащей прямой, принадлежит проекции.
этой прямой (рис. 1; рис.2)
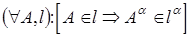
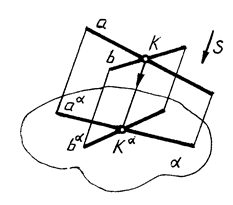
4. Проекция точки пересечения прямых определяется пересечением проекций этих прямых (рис. 3)
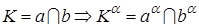
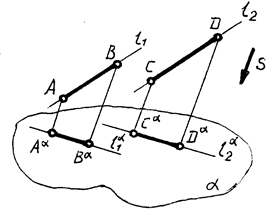
5. Проекции взаимно параллельных прямых взаимно параллельны (рис. 4)
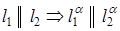
6. Отношение длин отрезков взаимно параллельных прямых равно отношению длин их проекций (рис. 4)
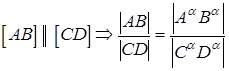
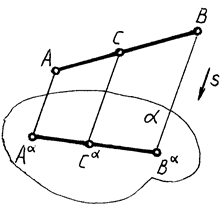
СЛЕДСТВИЕ: если отрезок прямой делится точкой в каком-либо отношении, то проекция отрезка делится проекцией этой точки в том же отношении (рис. 5)
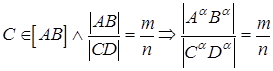
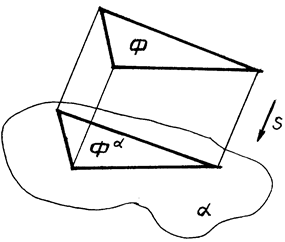
7. Плоская фигура, параллельная плоскости проекций, проецируется на эту плоскость в конгруэнтную фигуру (рис. 6)
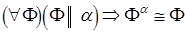
| Рис. 3 Рис. 4 |
| Рис. 5 Рис. 6 |
Date: 2015-04-23; view: 790; Нарушение авторских прав