Основные теоретические положения. В данной работе исследуется неразветвленная цепь, состоящая из катушки индуктивности и конденсатора
В данной работе исследуется неразветвленная цепь, состоящая из катушки индуктивности и конденсатора, подключенная к сети синусоидального тока. Схема цепи представлена на рис. 1.
Реальная катушка индуктивности обладает, кроме индуктивного сопротивления XL, еще я активным сопротивлением R, которое существенно влияет на протекающие в цепи процессы. Поэтому целесообразно реальную цепь представить в видесхемы замещения (рис. 2), где катушка индуктивности рассматривается как последовательное соединение резистивного элемента с активным сопротивлением R. и индуктивного элемента с индуктивностью L. При этом, падение напряжения на катушке UК равно сумме падений напряжений на резистивном элементе UR и индуктивном элементе UL.
Индуктивный и емкостный элементы характеризуются соответственно индуктивным XL = wL [Ом] и емкостным XC = 1/wC [Ом] сопротивлениями,
где: w=2pf [с-1] – угловая частота; f [Гц] - частота тока в цепи (f=50 Гц).
Величина X = XL – XC, называется реактивным сопротивлением. Соотношение активного R, реактивного X и полного Z сопротивлений определяется треугольником сопротивлении (рис.3), т.е.
Z = 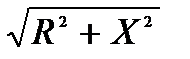 или Z = или Z = 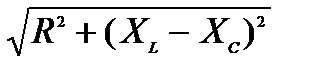 . .
Кроме того, справедливо: R=Z*cos j, X= Z*sin j j= arctg (X/R).
Аналогичный треугольник связывает вектора: напряжения U всей цепи, напряжения U R на активном сопротивлении цепи, и напряжения U X на реактивном сопротивлении цепи, действующее значение которого определяется формулой UX=UL–UC (рис.4).
Кроме того, соотношения между полной S (мощностью всей цепи), активной P (мощностью на активных элементах цепи) и реактивной Q =QL – QC (мощностью на реактивных элементах цепи), также определяется треугольником (рис.5).
Отметим, что угол j = jU – jI называется углом сдвига фаз и является одним из важнейших параметров цепей переменного синусоидального тока. Он показывает разницу между начальными фазами векторов напряжения – jU и тока – jI, и одинаков для всех приведенных треугольников. Это свойство цепей переменного тока значительно облегчает их расчет, так как многие параметры цепи могут быть найдены из геометрических соотношений.
Необходимо отметить, что:
· вектор напряжения U R совпадает по фазе с вектором тока I. Действующее значение этого напряжения UR = R*I;
· вектор напряжения U L опережает по фазе вектор тока I на угол p/2. Действующее значение этого напряжения UL = XL*I;
· вектор напряжения U C отстает по фазе от вектора тока I на угол p/2. Действующее значение этого напряжения UC = XC*I.
Таким образом, возможны три режима работы цепи переменного синусоидального тока, определяемые соотношением между величинами индуктивного XL и емкостного XC сопротивлений:
XL > XC, тогда UL > UC, и вектор напряжения U опережает по фазе вектор тока I на угол j, лежащий в пределах 0 < j < p/2.Такая цепь (нагрузка) называется активно-индуктивной (рис. 6).
XL < XC, тогда UL < UC, и вектор напряжения U отстает по фазе от вектор тока I на угол j, лежащий в пределах -p/2 < j < 0.Такая цепь (нагрузка) называется активно-емкостной (рис. 7).
XL = XC, тогда UL = UC, и вектор напряжения U совпадает по фазе с вектором тока I. Угол j=0. Такой режим работы последовательной цепи синусоидального тока называется резонансом напряжений (рис. 8).
Из выражения
XL = XC или wL = 1/wC
следуют условия, с помощью которых можно добиться возникновения резонанса в цепи:
1. путем подбора частоты wрез = 1/ 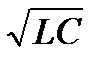 питающего напряжения; питающего напряжения;
2. путем подбора индуктивности Lрез = 1/w2C катушки;
3. путем подбора емкости Cрез = 1/w2L конденсатора (в данной работе резонанса добиваются именно этим способом).
Очевидно, что при резонансе напряжений величина реактивного сопротивления Xрез = XL – XC равна нулю, а полное сопротивление цепи Zрез = R. Поэтому, действующее значение резонансного тока (величина которого максимальна) определяется формулой:
Iрез = U/Zрез = U/R max.
При этом, вектора напряжений U L и U C на реактивных элементах достигают величин UL = Iрез XL и UC = Iрез XC, численно равны между собой, и противоположны по направлению. Следовательно напряжение цепи, при резонансе напряжений, равно напряжению на активном элементе т.е. U = UR (рис. 8). Отметим, что при условии R<<XL(C) (имеющим, как правило, место в цепях содержащих только катушку индуктивности и емкость) напряжение на реактивных элементах будут во много раз превышать напряжение на зажимах цепи, т.е. U<<UL(C).
Полная мощность последовательной цепи синусоидального тока может быть определена по одной из следующих формул:
S = UI, S = ZI2, S = 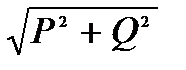 ; ;
соответственно активная мощность:
P = UR I, P = RI2, P = UI cos j, P = S cos j;
и реактивная мощность:
Q = QL - QC = (UL - UC) I, Q = XI2 = (XL -XC) I2, Q = UI sin j, Q = S sin j.
Величина cos j= P/S называется коэффициентом мощности. Она показывает какую часть от полной мощности S составляет мощность P, выделяемая на активных элементах цепи.
В режиме резонанса напряжений QL = QC, следовательно полная мощность цепи будет равна активной мощности Sрез= P, а cos j= cos 0 = 1.
Date: 2015-05-22; view: 615; Нарушение авторских прав | Понравилась страница? Лайкни для друзей: |
|
|



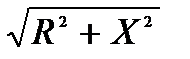 или Z =
или Z = 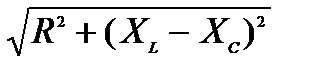 .
.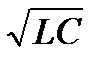 питающего напряжения;
питающего напряжения;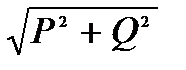 ;
;