Теория вероятностей и математическая статистика

Нормальным называют распределение вероятностей непрерывной случайной величины Х, плотность которого имеет вид

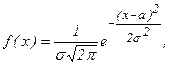
где а – математическое ожидание, σ – среднее квадратическое отклонение Х.

Вероятность того, что Х примет значение, принадлежащее интервалу (α,β),

Р(α<х<β)=Ф 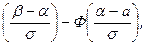(1)

где Ф(х)= 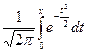- функция Лапласа.

Пример 1. Математическое ожидание а нормально распределенной случайной величины Х а=10, среднее квадратическое отклонение σ= 2. Найти вероятность попадания этой величины в интервал (12;14).

Решение: Подставив в формулу (1) α=12, β=14, а=10, σ=2, получаем

Р(12<х<14)=Ф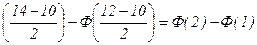

По таблице для функции Лапласа находим, что Ф(2)= 0,4772, Ф(1)=0,3413 и искомая вероятность Р(12<х<14)=0,1359.

Оценки, которые определяются одним числом, называют точечными. При малом числе наблюдений эти оценки могут приводить к грубым ошибкам. Чтобы избежать этих ошибок, используют интервальные оценки, которые определяются двумя числами – концами интервала (в котором заключена оцениваемая величина с заданной вероятностью).

Таким образом, задача сводится к отысканию такого интервала (его называют доверительным), который с заданной вероятностью γ (ее называют надежностью) покрывают оцениваемый параметр. Наиболее часто надежность принимают равной 0,95 или 0,99, или 0,999.

В частности, при надежности γ=0,95 доверительный интервал для оценки математического ожидания а нормального распределения (по выборочной средней 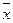выборки объема n, при известном σ) находят по формуле

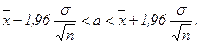
В обозначениях формула принимает вид: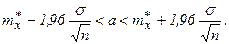

Если доверительный интервал найден, то с надежностью 0,95 можно считать, что оцениваемый параметр заключен в этом интервале.

Пример 2. Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 0,95, зная выборочную среднюю 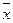=10,43 (статистическую среднюю 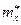), объем выборки (число наблюдений) n=100 и среднее квадратическое отклонение σ=5.

Решение: Воспользуемся формулой:

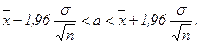
Подставляя данные, получаем:

10,43-1,96(5/10)< а <10,43+1,96(5/10), или окончательно 9,45< а <11,41.

Date: 2015-04-23; view: 513; Нарушение авторских прав