Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Пример 12
|
|
Построить фундаментальную систему решений однородной системы линейных уравнений:
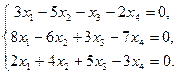
Решение
Выясним ранг системы, т.е. запишем матрицу
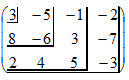
| и вычислим миноры: |
; 
;
;
.
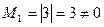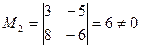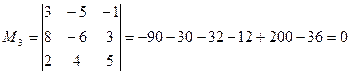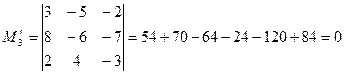Следовательно, ранг системы равен 2, т.е.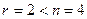 
. А значит, система имеет ненулевые решения и, по теореме 2 фундаментальная система решений будет состоять из 
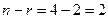линейно независимых решений. При этом базисный минор 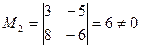и тогда однородная система равносильна системе из 2-х уравнений:
где 
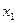и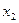 
(при базисном миноре) являются основными (или базисными) переменными, а 
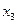и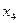 
– свободными, принимающими любые действительные значения.
По формуле Крамера находим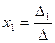 
и 
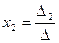, где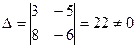 
,
, 
.
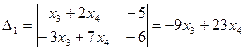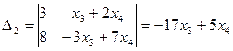Получаем решение исходной однородной системы в виде
; 
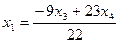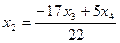, где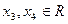 
. Полагаем для свободных переменных 
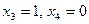и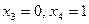 
и находим 2 линейно независимых решения: 
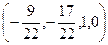и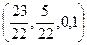 
.
|
|
|
|
|
| 
| 
| 
|
| 
|
|
|
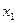
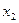
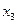
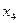
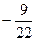
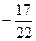
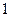
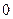
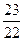
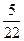
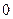
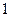
Все решения однородной системы получаются как линейная комбинация: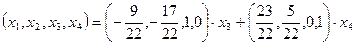 
; 
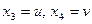– любые действительные числа.
Замечание. Геометрически полученное решение в 4-х мерном пространстве изображается 2-х мерной плоскостью, т.к. ее параметрические уравнения имеют вид:
, 
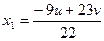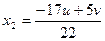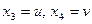, , где 
.
Date: 2015-04-23; view: 596; Нарушение авторских прав