Метод Жордановых исключений

В основе метода Жордановых исключений лежат элементарные преобразования типа Гаусса, с помощью которых приводим матрицу системы к единичной 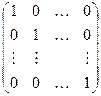. Тогда расширенная матрица СЛАУ

примет вид: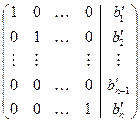

.

Автоматически получим решение СЛАУ: 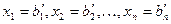(см. пример 11).

При решении СЛАУ методом Жордановых исключений удобно расширенную матрицу системы записывать в виде следующей таблицы:

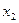
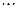
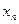
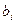
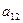
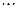
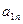
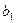
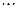
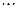
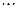
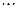
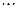
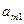
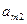
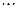
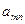
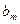
1.9. Ранг матрицы. Теорема Кронекера – Капелли

Наивысший порядок отличных от нуля миноров матрицы называется рангом этой матрицы и обозначается 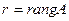. Для вычисления ранга матрицы применяем метод окаймляющих миноров.

Например, задана матрица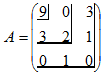

Находим ее окаймляющие миноры:

; ; .

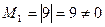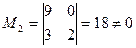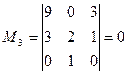Окаймляющий минор 3-го порядка равен нулю, следовательно ранг равен порядку предыдущего минора 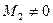, т. е. .

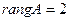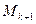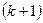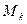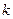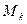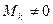Замечание. Минор порядка , содержащий в себе минор порядка , называется окаймляющим минором . Если у матрицы найдется минор , а все окаймляющие его миноры 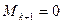, то .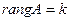

Рассмотрим произвольную систему вида (16)

Основная матрица этой системы 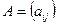, а расширенная 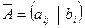, где 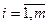_, . Система (16) будет совместной (т.е. будет иметь решение) тогда и только тогда, когда ранг матрицы системы совпадает с рангом расширенной матрицы этой системы, т.е.

.

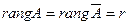Это и есть теорема Кронекера–Капелли.

Для ранга системы возможны два случая:

1) если общий ранг равен числу неизвестных 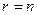, то система (16) будет иметь единственное решение;

2) если 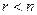, то система (16) будет иметь бесконечное число решений.

Если же 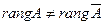, то система (16) несовместна, т.е. не имеет решений.

Date: 2015-04-23; view: 2784; Нарушение авторских прав