Пример 11

Выяснить совместность системы и найти ее решение.

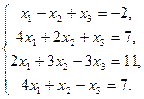
Решение

Система является переопределенной: число уравнений 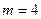больше числа неизвестных 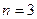. Запишем основную и расширенную 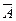матрицы системы:

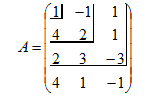
и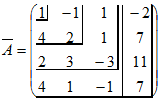

Методом окаймляющих миноров найдем ранги этих матриц:

, , .

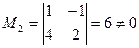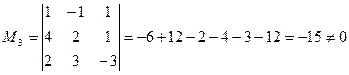Так как основная матрица не имеет минора 4-го порядка, то ее ранг равен 3, т.е. .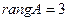

Для расширенной матрицы считаем окаймляющий минор:

.

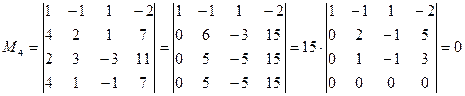Следовательно, ранг расширенной матрицы 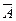равен 3, т.е. 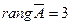. Тогда, по теореме Кронекера–Капелли, исходная система имеет единственное решение, т.к. .

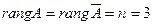Найдем это решение методом Жордановых исключений:

+ ~ ~

~ + ~ – + ~ ~

~

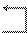
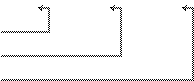
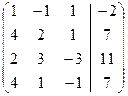
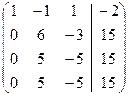
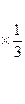
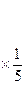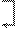
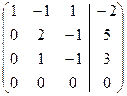
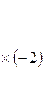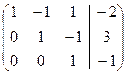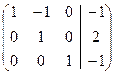
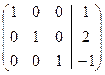
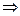
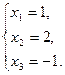
Ответ: система имеет единственное решение .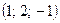

1.10. Однородные системы

Система вида

, (17)

где 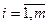_, называется однородной. Она всегда совместна, поскольку набор значений неизвестных удовлетворяет всем уравнениям системы. Это решение называется тривиальным, в остальных случаях:

1) однородная система будет иметь ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных;

2) если в однородной системе число уравнений меньше числа неизвестных, то система имеет ненулевое решение;

3) однородная система, в которой число уравнений равно числу неизвестных, имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю;

4) пусть наборы 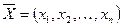и 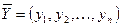являются решениями однородной системы, тогда их линейная комбинация 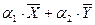– также решение однородной системы (17).

Из числа решений однородной системы (17) всегда можно построить конечную линейно независимую систему решений, причем такую, что всякое другое решение системы (17) будет линейной комбинацией решений, входящих в эту построенную систему. Такую систему решений называют фундаментальной.

Теорема 2. Если ранг 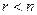, то всякая фундаментальная система решений однородной системы (17) будет состоять из 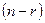решений.

Date: 2015-04-23; view: 744; Нарушение авторских прав
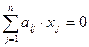