ЛЕКЦИЯ №10

Теория возмущений. МОЛЕКУЛа водорода

Многие задачи квантовой механики, связанные с рассмотрением многоатомных систем и др., сводятся к учету малых возмущений, вносимым взаимодействием подсистем, в энергию основного состояния всей системы. Основным подходом теории возмущений является построение волновой функции возмущенной системы через линейную комбинацию волновых функций всех возможных состояний невозмущенной системы. Рассмотрим этот подход на примере расчета спектра молекулы водорода.

Энергия молекул содержит не только энергию электронов, но и энергию относительного движения ядер, энергию вращения молекулы, а также энергию магнитных взаимодействий магнитных моментов атомов, то есть магнитных моментов орбитального движения электронов и их спинов. Вклад магнитных взаимодействий значительно меньше вклада электростатических взаимодействия и его рассматривать не будем.

Далее введем адиабатическое приближение, в котором расчет энергии электронов в молекуле ведется в пренебрежении движением ядер, а расчет энергии движения ядер не учитывает реакции электронов. В этом приближении гамильтониан электронов в молекуле водорода имеет вид:

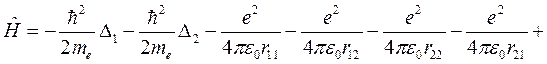
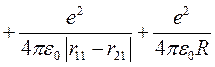, (10.1)

где r_ij – расстояние между i -м электроном и j -м ядром (протоном), R – расстояние между протонами, которое считается постоянным. Выберем начало координат на первом протоне, тогда координаты первого и второго электронов r₁ и r₂ связаны с расстояниями r_ij очевидными соотношениями:

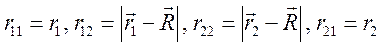
Предполагая, что оба электрона находятся в состоянии 1s, запишем для них на основании (9.9) одночастичные волновые функции относительно каждого из протонов:

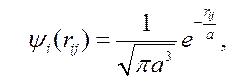
Из этих функций строятся симметричная и антисимметричная волновые функции системы из двух электронов в так называемом нулевом приближении теории возмущений, то есть в пренебрежении взаимодействием (отталкиванием) электронов и ядер (последние два положительных слагаемых в (10.1)):

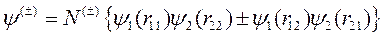, (10.2)

где N ^(±) – нормировочный множитель. Симметричному состоянию, когда спины электронов параллельны, соответствует выбор знака «+», а антисимметричному состоянию с антипараллельными спинами соответствует знак «–». В этом приближении энергия электронов в молекуле Е ⁽⁰⁾ равна сумме энергий для изолированных атомов, то есть в основном состоянии Е ⁽⁰⁾=2´(-13.55)= -27.1 эВ.

Определим нормировочный множитель N ^(±), требуя нормировки (10.2) на единицу:

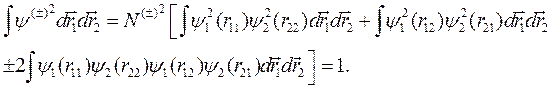
Поскольку одночастичные функции нормированы на 1, два первых интеграла равны 1 каждый, тогда получим:

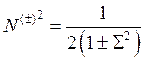, (10.3)

где

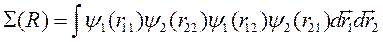(10.4)

называется интеграл перекрытия волновых функций.

Для получения первого приближения теории возмущений, то есть определения энергии Е ⁽¹⁾, нужно вычислить среднее значение гамильтониана (10.1) в волновых функциях нулевого приближения (10.2):

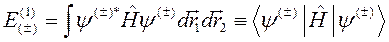. (10.5)

Второе приближение вычисляется в волновых функциях первого приближения, третье – в волновых функциях второго и т.д. Ограничимся, однако, только первым приближением. Вычисление (10.5) дает:

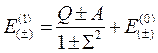, (10.6)

где

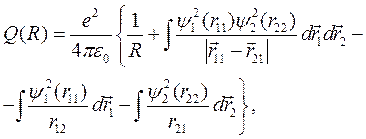(10.7)

– энергия кулоновского взаимодействия всех частиц в молекуле водорода,

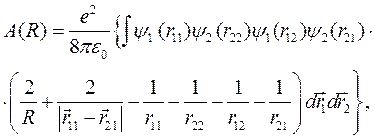(10.8)

– обменная энергия электронов, обусловленная обменным взаимодействием.

Разность энергий первого и нулевого приближений определяет в первом приближении энергию связи электронов в молекуле водорода:

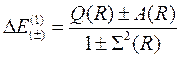(10.9)

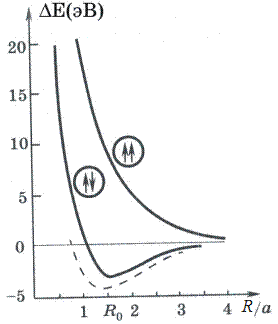Очевидно, она зависит от выбора знака в формуле (10.9), то есть от симметрии волновой функции, которая в свою очередь определяется взаимной ориентацией спинов электронов. На рис. 10.1 представлены расчетные (сплошные) и экспериментальная (штриховая) зависимости энергии связи от расстояния между ядрами для двух возможных взаимных ориентаций спинов. Видно, что при параллельной ориентации, то есть когда проекция полного спина S=1, энергия связи положительна, что соответствует отталкиванию атомов друг от друга. При антипараллельной ориентации спинов, когда S=0, энергия связи может быть положительной и отрицательной с минимумом Δ Е ₀ ≈ -3 эВ при некотором расстоянии между ядрами R ₀, называемом равновесным. Характерно, что расстояние между атомами в молекуле меньше двух радиусов отдельных атомов (R ₀ ≈ 1.6 а ≈ 0.08 нм).

Рассмотрим теперь движение ядер (протонов) в пренебрежении реакцией электронов. Протоны могут совершать вращательное движение вокруг центра масс и колебательное движение в направлении друг друга. Поэтому уравнение Шредингера должно содержать оператор квадрата момента импульса и потенциальную энергию квантового осциллятора. Поскольку оператор квадрата момента импульса коммутирует с гамильтонианом, то аналогично задаче об атоме водорода волновая функция системы двух протонов должна содержать шаровую функцию и радиальную функцию. Запишем тогда эту волновую функцию в виде:

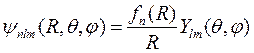, (10.10)

где R – расстояние между протонами. Тогда для радиальной функции f (R) уравнение Шредингера дает:

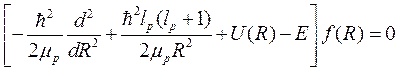, (10.11)

где m_p = m_p /2 – приведенная масса двух протона, l_p – орбитальное число для протонов, а потенциальная энергия квантового осциллятора

,

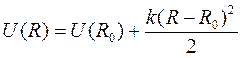где R ₀ – точка минимума потенциальной энергии колебаний протонов. Будем считать колебания протонов малыми, тогда, полагая R ≈ R ₀, уравнение (10.11) можно представить в виде уравнения гармонического осциллятора

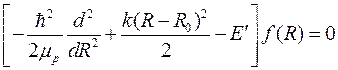, (10.12)

где

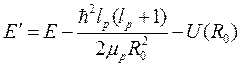. (10.13)

Как известно, энергия гармонического квантового осциллятора принимает значения:

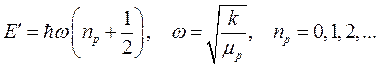(10.14)

Потенциальная энергия электронов молекулы водорода при полном спине S=0 получается, если сложить энергию электронов, определяемую по формуле (10.6) и добавить энергию связи электронов Δ Е ₀ ≈ -3 эВ:

.

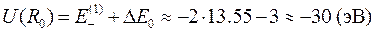Тогда полная энергия молекулы водорода в 1s- состоянии равна:

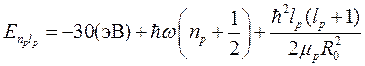, (10.15)

Для молекулы водорода известны следующие экспериментальные значения:

, ,

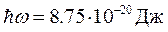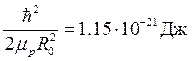поэтому энергии колебаний протонов и, тем более, энергии вращения молекулы как целого значительно меньше энергии электронов (1 эВ=1.6×10^-19Дж).

Полный спектр молекулы водорода можно получить, подставив вместо U (R ₀) энергию электронных термов (9.10) с поправкой (10.6), зависящей от орбитального числа для возбужденных состояний, то есть:

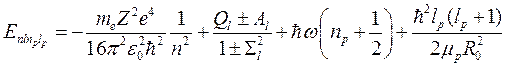(10.16)

В формуле (10.16) отчетливо видно, что полный спектр молекулы складывается из электронного спектра – первые два слагаемых, колебательного спектра ядер (третье слагаемое) и вращательного спектра (четвертое слагаемое). По энергетическому интервалу эти спектры располагаются в таком же порядке от большего к меньшему. То есть внутри энергетических интервалов между электронными уровнями располагаются эквидистантные колебательные уровни, а между колебательными уровнями располагаются вращательные уровни, «разбегающиеся» от соответствующих колебательных уровней (рис. 10.2).

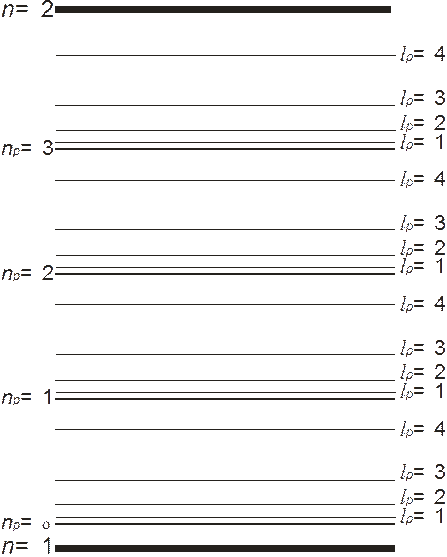
Рис. 10.2. Схематическое изображение уровней энергии молекулы водорода

при 1s-состояниях электронов

В возбужденных электронных состояниях, когда орбитальное квантовое число l > 0 спектр энергий молекулы, очевидно, становится значительно сложнее.

Date: 2015-05-19; view: 406; Нарушение авторских прав