Квантовый осциллятор. В классической механике, как известно, линейная гармоническая колебательная система (осциллятор) образуется при наличии инерциального элемента (груза массой

В классической механике, как известно, линейная гармоническая колебательная система (осциллятор) образуется при наличии инерциального элемента (груза массой m) и «возвращающей» силы, пропорциональной смещению груза от положения равновесия. В кристаллической решетке роль инерциальных элементов играют ионы, а «возвращающая» сила возникает при отклонении иона от положения равновесия вследствие локального нарушения электронейтральности и электростатического взаимодействия. В простейшем случае для линейной «возвращающей» силы 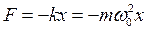зависимость электрической потенциальной энергии иона от смещения будет квадратичной (по аналогии с классическим осциллятором, например, пружинным маятником) и может быть записана (для одномерного движения) в виде:

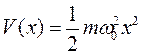, (6.1)

где ω₀ – собственная частота осциллятора. В этом случае для квантового осциллятора (иона в кристаллической решетке) можно получить аналитическое решение в специальных функциях. Уравнение Шредингера

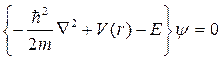(6.2)

можно переписать в виде

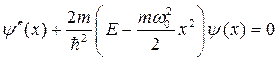. (6.3)

Для решения этого уравнения введем безразмерные величины

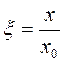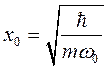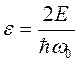, , (6.4)

и после элементарных преобразований уравнение (8.3) приводится к виду

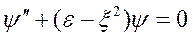(6.5)

Требуется найти конечные, непрерывные и однозначные решения этого уравнения в интервале – ∞< x < + ∞. Такие решения уравнение (6.5) имеет не при всех значениях параметра ε, а лишь при

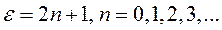(6.6)

причем соответствующие функции ψ_n равны

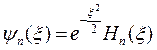(6.7)

где Н_п(x) есть полином Чебышева — Эрмита n -го порядка, определяемый формулой

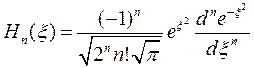(6.8)

при этом множитель обеспечивает нормировку на 1:

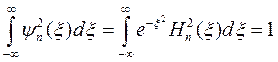(6.9)

Таким образом, одного требования непрерывности и конечности ψ оказывается достаточно, чтобы параметр ε получал лишь дискретные значения (6.6). Но согласно (6.4) этот параметр определяет энергию. Сравнивая (6.4) и (6.6), находим, что возможные значения Е_п суть

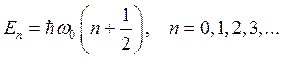. (6.10)

Эта формула показывает, что энергия осциллятора Е может иметь лишь дискретные значения. Число п, определяющее номер квантового уровня, называют главным квантовым числом.

Квант колебаний иона называется фононом. Формула (6.10) показывает, что в наинизшем состоянии (n =0), соответствующем температуре абсолютного нуля, движение не исчезает и ионы кристаллической решетки совершают так называемые «нулевые» колебания, которые упрощенно можно характеризовать частотой w₀ /2, имея в виду, что согласно принципу неопределенности, связывающему неопределенности энергии и периода колебаний (3.2), регулярный колебательный процесс ионов невозможен. При увеличении температуры кристаллической решетки занимаются состояния с n >1 и возникает распределение фононов по энергиям.

Решение уравнения Шредингера (6.3) в окончательном виде есть

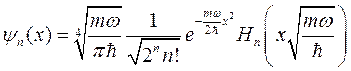, (6.11)

где Н_n (х) – полиномы Эрмита. Выпишем несколько первых полиномов:

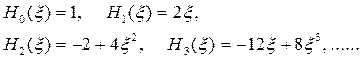(6.12)

Таким образом, волновая функция основного состояния (n =0)

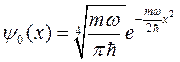
симметрична и не имеет нулей. В этом состоянии ионы совершают колебания с энергией

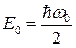, (6.13)

а поскольку неопределенность энергии (6.13) мала, то период колебаний имеет большую неопределенность, так что говорить о регулярных колебаниях нельзя. В этом случае говорят о флуктуационных колебаниях.

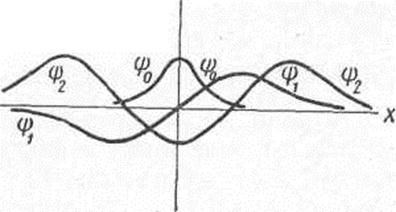
На основании (6.11) и (6.12) волновые функции при четных n – четные, а при нечетных n – нечетные. Графики трех первых волновых функций показаны на рис. 6.1.

Рис. 6.1. Волновые функции квантового осциллятора

На рис. 6.2 приведена потенциальная функция гармонического осциллятора и дискретный набор значений энергии (уровни энергии). По оси ординат отложена потенциальная энергия, а по оси абсцисс отклонение х. На этом же рисунке горизонтальными линиями изображены уровни энергии Е_п (6.10) для разных п.

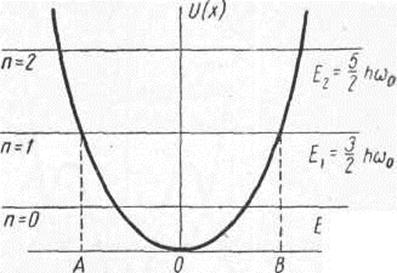
Рис. 6.2. Потенциальная энергия и энергетические уровни квантового осциллятора

Рассмотрим, например, уровень Е₁. Согласно классической механике частица, имеющая энергию Е₁ могла бы быть обнаружена лишь в области АВ. В самом деле, А и В только точки, где потенциальная энергия равна полной. В этих точках кинетическая энергия Т равна нулю. Точки А и В называются точками поворота. А квантовая частица с отличной от нуля вероятностью может находиться вне пределов области АБ, что видно из графика волновой функции y₁ (рис. 6.1).

Date: 2015-05-19; view: 441; Нарушение авторских прав