Оператор момента импульса. Спин

Движение частицы по прямой характеризуется импульсом. При отсутствии внешних воздействий на частицу или систему свободно движущихся частиц импульс сохраняется, то есть

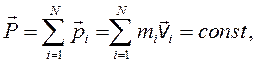
а его величина, как собственное значение оператора импульса, может принимать любые значения.

Если частица движется по криволинейной замкнутой траектории, ее движение характеризуется моментом импульса:

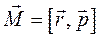, (8.1)

В классической механике эта величина также сохраняется (является интегралом движения) и может принимать произвольные значения. Например, при движении спутника по высокоэллиптической орбите импульс не сохраняется, так как скорость спутника меняется в зависимости от расстояния до Земли, но момент импульса сохраняется.

В квантовой механике момент импульса «квантуется», то есть может принимать только дискретные значения, пропорциональные постоянной Планка 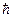, имеющей размерность момента импульса. Это было гениальной догадкой Н.Бора, которую он ввел, как постулат. Покажем это, исходя из других, принятых позднее, постулатов квантовой механики.

В квантовой механике оператор момента импульса определяется в соответствии с третьим постулатом по классическому выражению (8.1) и имеет вид:

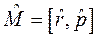(8.2)

Как у вектора 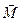из (8.1) есть компоненты М_х, М_у и М_z, так и у оператора 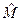определяются операторы проекций на оси координат 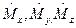, задаваемые формулами проекций векторного произведения:

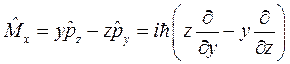
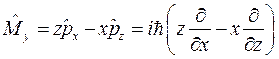(8.3)

.

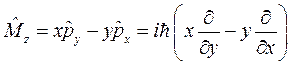Нетрудно показать, что проекции оператора момента не коммутируют друг с другом:

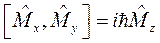, (8.4)

а два других коммутатора получаются циклической перестановкой координат. Это означает, что они одновременно не измеримы, то есть, если определена или задана одна проекция оператора момента, то две других проекции не имеют определенного значения.

Определим также оператор квадрата момента импульса:

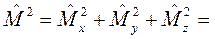
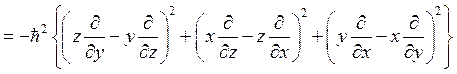(8.5)

Но этот оператор, как нетрудно показать, коммутирует с любым оператором проекции:

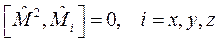, (8.6)

что означает их одновременную измеримость, а также наличие общей системы собственных функций. Таким образом, если измерена (задана) одна проекция момента импульса на некоторую выбранную ось, то две других проекции могут иметь любые значения. То есть, как и должно быть в соответствии с принципом неопределенности, невозможно точно задать пространственную ориентацию вектора момента импульса, а лишь можно сказать, что он локализован в пределах некоторой конической поверхности (см. ниже рис. 8.1).

Вращательное движение удобнее описывать в сферической системе координат. Переход из декартовой системы в сферическую дается формулами:

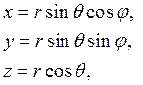
тогда операторы проекций момента и квадрата момента имеют вид:

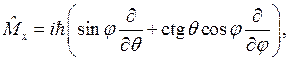(8.7х)

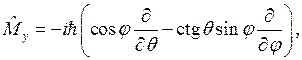(8.7у)

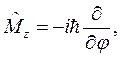(8.7z)

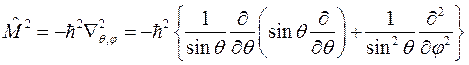, (8.8)

где оператор 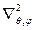называется сферическим оператором Лапласа. Все эти операторы не действуют на координату r, а действуют только на угловые координаты, следовательно, их собственные функции могут зависеть только от угловых координат, то есть

,

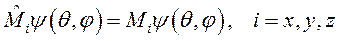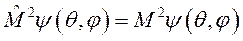. (8.9)

Введя обозначение

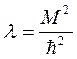, (8.10)

получим из (8.9) уравнение для функции y:

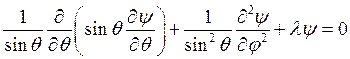(8.11)

Это уравнение имеет решение только при 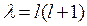(l =0,1,2,3,…) в специальных функциях, называемых сферическими гармониками или шаровыми функциями, причем для каждого значения l имеется 2 l +1 решений:

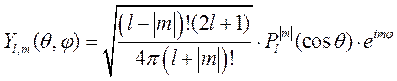. (8.12)

Здесь целое число m принимает 2 l +1 значений: m = 0, ±1, ±2, ±3, …, ± l. Таким образом, каждому собственному значению оператора квадрата момента

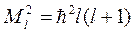(8.13)

соответствует не одна, а набор из 2 l +1 собственных функций

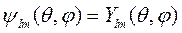(8.14)

Такая ситуация называется вырождением.

Шаровые функции для l =0,1,2 имеют вид:

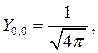
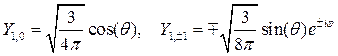
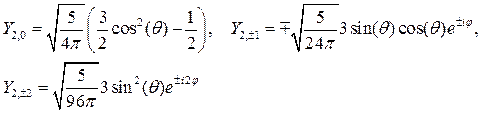
На основании (8.6) собственные функции (8.14) являются также собственными функциями операторов проекций момента. Рассмотрим оператор 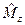. Функции (8.14) удовлетворяют уравнению

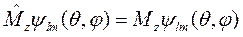(8.15)

или, расписывая выражение для оператора и производя дифференцирование, получим

,

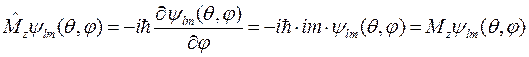откуда собственное значение

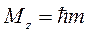(8.16)

Отсюда следует, что состояния 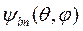при заданном полном моменте 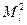(задано l) описывают состояния с различными проекциями момента на ось z, характеризуемые числом m. Таким образом, возможные значения абсолютной величины момента импульса и возможные значения проекции момента импульса на произвольную ось z имеют квантованные значения. Никакие другие значения, кроме приведенных, не могут реализоваться в природе.

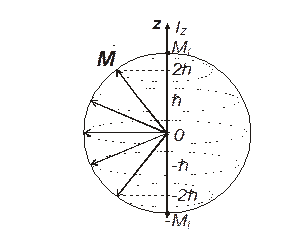Оператор 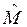называется оператором орбитального момента, его собственное значение

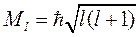(8.17)

определяется целым числом l, которое называется орбитальным квантовым числом. Собственное значение оператора 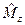(8.16) определяется целым числом m, которое называется магнитным квантовым числом.

В состояниях, в которых М² и М_z имеют определенные значения, проекции М_х и М_у не имеют определенных значений (кроме случая l =0). Это означает, что в соответствии с принципом неопределенности частица при вращательном движении, так же как и при поступательном, не локализована в точке, а вектор момента импульса равновероятно может иметь любое направление в пределах конической поверхности, определяемой проекцией на ось z (рис. 8.1).

При рассмотрении системы вращающихся частиц, например, электронной оболочки атома или атомного ядра, состоящих из многих электронов или нуклонов, для нахождения полного момента импульса системы 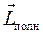нужно сложить моменты подсистем, составляющих систему. Рассмотрим, например, систему двух частиц, тогда

,

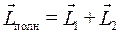а квантованные значения полного момента определяется следующим образом

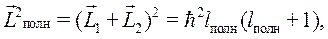
где 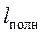может принимать следующие значения:

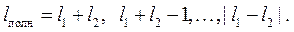(8.17)

Соотношение (8.17) называется правилом сложения моментов в квантовой механике.

Если частицу рассматривать классически как тело конечных размеров, то кроме орбитального движения возможно еще и собственное вращательное движение частицы вокруг собственной оси, характеризуемое собственным моментом импульса. Квантовомеханический аналог собственного момента импульса называется спином, оператор спина обозначается 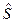. По аналогии с оператором момента импульса 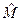вводится его собственное значение в виде

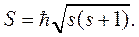(8.18)

Также вводится оператор проекции спина на выделенное направление 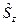, имеющий собственные значения

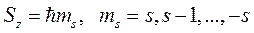. (8.19)

Квантовое число m_s принимает 2 s +1 значение, по которым различаются квантовые состояния. На основании экспериментов Штерна-Герлаха по расщеплению пучка атомов водорода в магнитном поле на два пучка следует, что для электрона возможны 2 различных состояния, то есть 2 s +1=2, откуда следует, что спиновое квантовое число для электрона s =1/2, а квантовое число проекции спина

.

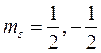Спиновый механический момент электрона всегда постоянен и равен

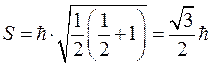, (8.20)

а в пространстве может иметь только два направления, соответствующих проекциям

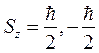. (8.21)

Отличие спина от классического собственного момента импульса выражается в том, что спин для конкретной частицы имеет постоянное значение, которое невозможно изменить, то есть спин является фундаментальной характеристикой частицы. Спиновое квантовое число s для разных частиц может принимать значения 0, 1/2, 1, 3/2,...

Полный механический момент электрона равен сумме орбитального и спинового моментов

.

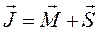На основании правила сложения моментов (8.17) собственное значение оператора 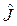изменяется в пределах 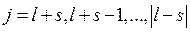. Так у электрона при l >0 может быть только 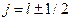, а при l =0 полный момент может иметь только одно собственное значение j =1/2.

Движение заряженных частиц по замкнутым траекториям кроме механического момента М характеризуется еще и магнитным моментом m, определяемым как произведение тока на площадь орбиты. Для круговой орбиты можно записать

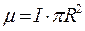, (8.22)

где R - радиус орбиты, а ток выражается формулой

,

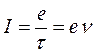где е - заряд частицы, t - время обращения по орбите, а n - частота этого вращения. Подставим последнее выражение в (8.22), умножим и разделим на массу частицы и, учитывая, что скорость частицы v=2pR/t =2pRv, получим

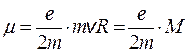, (8.23)

то есть магнитный момент заряженной частицы строго пропорционален ее механическому моменту М. Используя квантовомеханическое значение для орбитального механического момента (8.17), запишем магнитный момент орбитального движения для электрона:

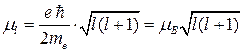, (8.24)

где величина 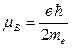= 9.27Ч10^-24 (Дж/Тл) - называется магнетоном Бора,

а для протона

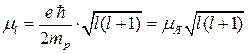, (8.25)

где 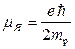=5.05Ч10^-27 (Дж/Тл) - называется ядерным магнетоном Бора, который в m_p / m_e =1836 раз меньше магнетона Бора. Поэтому магнитные свойства атомов определяются в основном магнитными свойствами его электронов. Нужно отметить, что при l = 0 у электрона отсутствуют механический момент импульса и магнитный момент, то есть он «не вращается» вокруг ядра, что невозможно в классическом случае.

Date: 2015-05-19; view: 520; Нарушение авторских прав