
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ЛЕКЦИЯ №9
|
|
УРАВНЕНИЕ ШРЕДИНГЕРА ДЛЯ ДВИЖЕНИЯ В ПОЛЕ
ЦЕНТРАЛЬНОЙ СИЛЫ
В классической механике кинетическая энергия криволинейного движения частицы имеет вид:
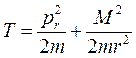 , (9.1)
, (9.1)
где pr – проекция импульса на радиус-вектор.
Для описания такого рода движения в квантовой механике нужно составить гамильтониан
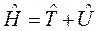 ,
,
где оператор кинетической энергии образуется из (9.1) заменой импульса на оператор импульса и квадрата момента импульса на соответствующий оператор, а потенциальная функция U (x,y,z) как правило, заимствуется из опыта и характеризует силовое поле, действующее на частицу.
Задача о движении в поле центральной силы решается в сферической системе координат. В этой системе координат оператор квадрата момента импульса выражен формулой (8.8), а радиальная часть оператора кинетической энергии имеет вид:
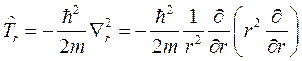 (9.2)
(9.2)
Таким образом, уравнение Шредингера для стационарных состояний движения в поле центральных сил имеет вид:
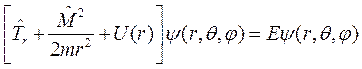 (9.3)
(9.3)
В этом уравнении первый и третий операторы зависят от радиуса, а второй оператор зависит только от угловых координат. Поэтому можно провести разделение переменных и, учитывая, что операторы 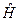 и
и 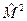 коммутируют, то есть имеют общую систему собственных функций, решение (9.3) нужно искать в виде:
коммутируют, то есть имеют общую систему собственных функций, решение (9.3) нужно искать в виде:
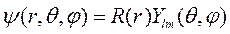 (9.4)
(9.4)
Умножим обе части (9.3) на r 2, преобразуем к выражению
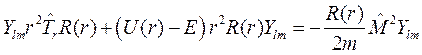
и разделим переменные. Для этого делим обе части на RYlm и учтем (8.13), тогда
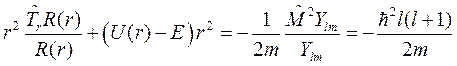
Окончательно для радиальной части решения – R (r), уравнение принимает вид:
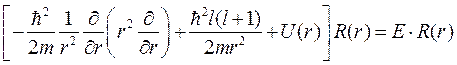 (9.5)
(9.5)
Рассмотрим движение электрона в атоме, где действует центральная кулоновская сила притяжения к ядру. Считая, что потенциальная энергия на бесконечности стремится к нулю, а притяжению соответствует отрицательная потенциальная энергия, потенциальную функцию для уравнения (9.5) представим в виде:
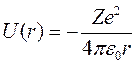 , (9.6)
, (9.6)
где Z – атомный номер или число протонов в ядре. Такой вид потенциальной функции используется только для так называемых водородоподобных атомов, к которым кроме водорода относится однократно ионизованный гелий (2Не+) и двукратно ионизованный литий (3Li++). В этих атомных системах в поле положительно заряженного ядра движется один электрон. В более тяжелых атомах нужно учитывать экранировку поля ядра другими электронами, при этом потенциальная функция становится более сложной. Таким образом, уравнение Шредингера для водородоподобного атома принимает вид:
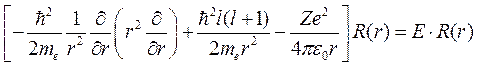 , (9.7)
, (9.7)
где введено обозначение массы электрона me.
Решение этого уравнения R (r) для отрицательных энергий (E <0) выражается через производные полиномов Лагерра, первые из которых имеют вид:
L0 (x)=1,
L1 (x)=1- x,
L2 (x)=(2-4 x+x 2)/2!,
L3 (x)=(6-18 x+ 9 x 2- х 3)/3!, …,
а полное частное нормированное решение уравнения Шредингера (9.3), то есть волновая функция электрона в водородоподобном атоме, с учетом угловой зависимости, описываемой шаровыми функциями, принимает вид:
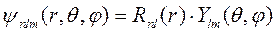 (9.8)
(9.8)
где
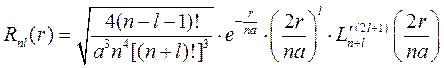 , (9.8а)
, (9.8а)
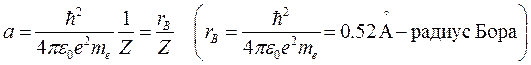 ,
,
n = n r + l +1, причем n r=0,1,2,…, l =0,1,2,…, n -1.
Таким образом, основное состояние атома описывается функцией
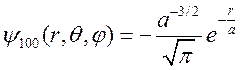 , (9.9)
, (9.9)
которая не зависит от углов и, следовательно, имеет сферическую симметрию. Для состояния (n =2, l =0, m =0) волновая функция
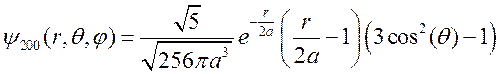 ,
,
имеет только азимутальную симметрию (по углу j), а в плоскостях, проходящих через ось z, определяет вытянутую вдоль этой оси область.
Собственные значения Е определяются в процессе решения из условия непрерывности и конечности R (r) для любых r. В области отрицательных значений энергии они дискретны и выражаются формулой:
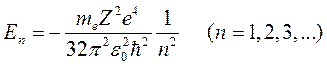 (9.10)
(9.10)
В области положительных энергий (Е >0) спектр водородоподобного атома непрерывный и простирается до бесконечности.
Число n =1,2,3,… определяет энергию электрона в атоме и называется главным квантовым числом.
Число n r=0,1,2,… определяет число нулей функции R (r) и называется радиальным квантовым числом.
Число l определяет момент импульса, который характеризует орбитальное движение, и поэтому называется орбитальным квантовым числом. Оно может принимать лишь следующие значения: l= 0,1,2,…, n -1.
Для каждого значения l существует 2 l +1 значений квантового числа m =0, 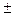 1,
1, 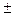 2,…,
2,…, 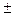 l, характеризующего количество пространственных ориентаций вектора момента относительно выделенной оси, его проекцию на эту ось, которая при приложенном магнитном поле совпадает с его направлением, и определяет взаимодействие магнитного момента движущегося электрона (пропорционального механическому моменту М) с магнитным полем. Поэтому это квантовое число называется магнитным квантовым числом.
l, характеризующего количество пространственных ориентаций вектора момента относительно выделенной оси, его проекцию на эту ось, которая при приложенном магнитном поле совпадает с его направлением, и определяет взаимодействие магнитного момента движущегося электрона (пропорционального механическому моменту М) с магнитным полем. Поэтому это квантовое число называется магнитным квантовым числом.
Определим кратность вырождения gn уровня энергии водородоподобного атома Еn. Для этого надо просуммировать все возможные состояния, определяемые орбитальным квантовым числом и умножить на два для учета вырождения по спину. Таким образом, получим:
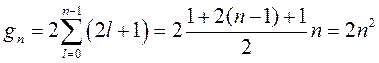 . (9.11)
. (9.11)
Следовательно, в первой оболочке, соответствующей главному квантовому числу n =1 (l =0), существуют два квантовых состояния, отличающихся проекциями спина, и может находиться 2 электрона, во второй оболочке (n =2, l =0,1) находится 8=2(1+3) электронов, в третьей (n =3, l =0,1,2) – 18=2(1+3+5) и т.д.
Таким образом, в рамках полученного решения уравнения Шредингера для центрально-симметричного кулоновского потенциала в водородоподобном атоме каждый возбужденный уровень энергии (n>1) многократно вырожден, то есть ему соответствует большое число квантовых состояний электрона, различающихся орбитальными и магнитными квантовыми числами или, проводя аналогию с классическим движением, различающихся формой и ориентацией орбит.
 В действительности, при учете магнитных взаимодействий внутри атома, а тем более при наличии внешних магнитных и электрических полей происходит снятие вырождения этих уровней, происходит расщепление одного уровня оболочки на 2 n 2 близко расположенных уровней.
В действительности, при учете магнитных взаимодействий внутри атома, а тем более при наличии внешних магнитных и электрических полей происходит снятие вырождения этих уровней, происходит расщепление одного уровня оболочки на 2 n 2 близко расположенных уровней.
Состояния с различными значениями l принято исторически обозначать буквой, соответствующей значению l, а именно
l= 0→ s – состояние,
l = 1→ р – состояние,
l = 2 → d – состояние,
l = 3 → f – состояние, и т.д.
Но для минимально необходимой характеристики состояния нужно еще указать главное квантовое число и тогда состояния, называемые термами, обозначаются следующим образом:
1s;
2s, 2p;
3s, 3p, 3d;
4s, 4p, 4d, 4f;
5s, 5p, 5d, 5f, 5i; …..

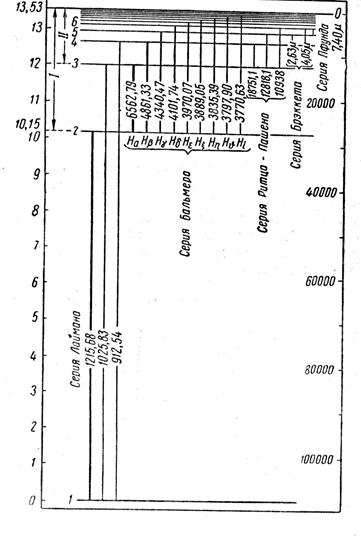
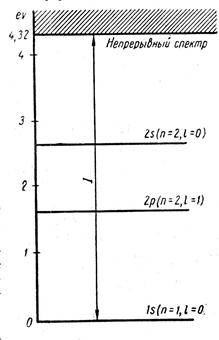
На рис.9.1. представлены, исходя из (9.10) при Z =1, уровни энергии атома водорода (в электронвольтах на левой шкале) для различных n. Эти уровни 2 n 2- кратно вырождены. Линии переходов содержат значения длины волны излучения (в ангстремах) для данного перехода.
Энергия ионизации водородоподобного атома, требуемая для удаления электрона с низшего энергетического уровня, равна
 . (9.12)
. (9.12)
В соответствии с постулатом Бора излучение (или поглощение) атома происходит при переходе электрона с одного уровня на другой, причем частота излучения определяется формулой:
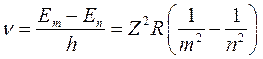 , (9.13)
, (9.13)
где
 (9.14)
(9.14)
постоянная Ридберга-Ритца, впервые теоретически вычисленная Н.Бором для атома водорода.
При более точном расчете водородоподобного атома с учетом конечности массы ядра необходимо рассматривать движение электрона и положительного ядра вокруг их центра масс. Тогда формула (9.14)переходит в формулу
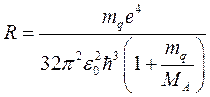 ,
,
где МА – масса центрального положительного заряда, mq – масса отрицательного заряда. Это особенно важно для таких квантовых систем, как мезоатом (вместо электрона – отрицательный мю-мезон с массой mq =207 mе), мюоний (вместо ядра – положительный мю-мезон с массой MA =207 mе) или позитроний (система из позитрона и электрона, МА = mq), где масса положительного ядра не так велика по сравнению с массой отрицательного заряда.
Из формулы для уровней энергии (9.10) при m =2 следует формула Бальмера, описывающая серию Бальмера на рис. 9.1, соответствующую переходам из высших возбужденных состояний на второй уровень (тоже возбужденный)
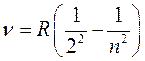 (9.15)
(9.15)
Серия Бальмера описывает спектральные линии, лежащие в основном в видимой области спектра. Переходы с возбужденных уровней на низший уровень Е 1, соответствующий основному (не возбужденному) состоянию, дают серию Лаймана, спектральные линии которой лежат в ультрафиолетовом диапазоне. Другие серии, соответствующие переходам между высшими возбужденными состояниями, описывают спектральные линии, лежащие в инфракрасном диапазоне.
В спектроскопии величину термов чаще указывают не в частотах, а в волновых числах, показывающих, сколько длин волн укладывается в 1 см. Поэтому «спектроскопическая частота» или волновое число, равное 1/l, определяется как:
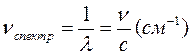 ,
,
то есть равна обычной частоте, деленной на скорость света с =3×1010(см/сек). На рис. 9.1 на правой шкале приведена шкала в этих единицах.
При дальнейшем развитии квантовой теории было показано, что возможны не любые переходы между стационарными квантовыми состояниями. Поскольку переход сопровождается излучением или поглощением фотона, который имеет спин S=1, то и в силу закона сохранения полного момента импульса системы изменение момента импульса атома при переходе может происходить только в такие состояния, для которых изменение орбитального квантового числа
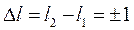
и магнитного квантового числа
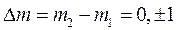 .
.
На изменение главного квантового числа n ограничений нет. Такие ограничения, накладываемые на изменение квантовых чисел при переходах между уровнями энергии называются правилами отбора.
Рассмотрим пространственное распределение плотности заряда электрона в различных квантовых состояниях. Для этого определим функцию распределения вероятности нахождения электрона в пространстве. Вероятность обнаружить электрон в сферическом элементе объема dV = r2 sin(θ) drdθdj определяется очевидной формулой
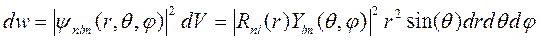 , (9.16)
, (9.16)
 |
из которой видно, что вероятность электрону находиться в ядре (при r =0) равна нулю, так как волновая функция ограничена везде.
 |
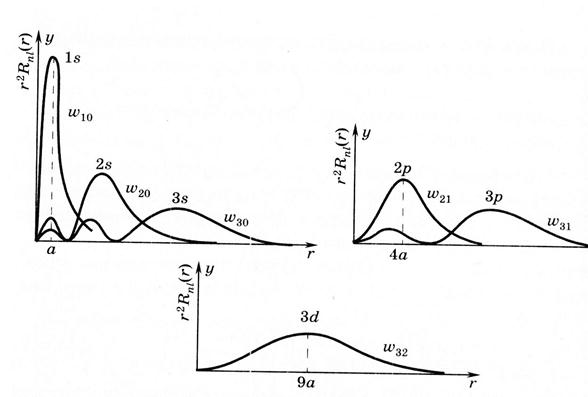
На основе выражения для радиальной части волновой функции (9.8а) интегрированием по угловым координатам (9.16) определяется радиальная зависимость вероятности w (r) или пропорциональной ей плотности заряда для различных состояний, что графически представлено на рис. 9.2.
Угловое распределение (по θ) плотности заряда, описывающее форму электронных облаков в пространстве, имеющих осевую симметрию относительно оси z (в силу независимости плотности вероятности от азимутального угла j) для максимального значения Rnl (r) показано на рис. 9.3.
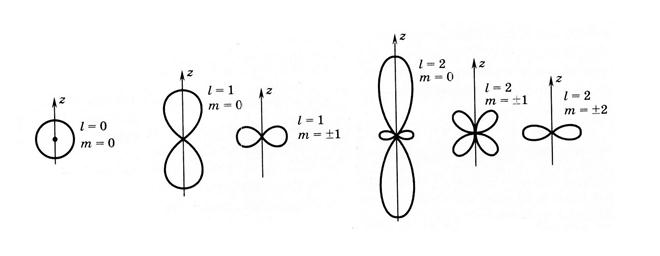
Рис. 9.3. Угловое распределение электронной плотности
в первых состояниях атома водорода
Для атомов щелочных металлов (3Li, 11Na, 19K, 29Cu, 47Ag, 55Cs, 79Au), имеющих один валентный электрон, расчет его спектра можно провести по описанной методике, но с учетом экранировки электрического поля ядра внутренними электронами. В этих атомах все внутренние оболочки полностью застроены и можно считать, что они образуют сферический слой отрицательного заряда, имеющего величину
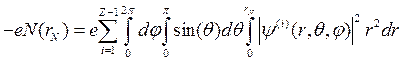
 ,
,
где rN – приближенный радиус оболочки внутренних электронов. Если считать, что валентный электрон находится далеко от этой оболочки, что является грубым приближением, то можно считать, что на этот электрон действует центральное поле с потенциалом
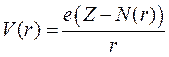 .
.
В этом приближении рассчитываются поправки Ридберга Δ l к главному квантовому числу
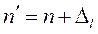 .
.
 Эти поправки зависят от орбитального квантового числа, что связано с разной конфигурацией электронных облаков или, как говорят, орбиталей, и, следовательно, пространственным распределением заряда для разных l. Поэтому в спектре атомов щелочных металлов снимается вырождение по l и термы имеют вид:
Эти поправки зависят от орбитального квантового числа, что связано с разной конфигурацией электронных облаков или, как говорят, орбиталей, и, следовательно, пространственным распределением заряда для разных l. Поэтому в спектре атомов щелочных металлов снимается вырождение по l и термы имеют вид:
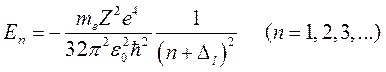 (9.17)
(9.17)
На рис. 9.4. приведен спектр калия, в котором видно значительное расхождение уровней 2s и 2p, хотя для атома водорода неразличимы.
Для многоэлектронных атомов поправки Ридберга рассчитать довольно сложно, они также зависят и от спина, поэтому используют их значения, определенные из спектроскопических экспериментов.
Date: 2015-05-19; view: 450; Нарушение авторских прав