Атом водорода. На основании своих исследований Резерфорд в 1911 г

На основании своих исследований Резерфорд в 1911 г. предложил ядерную (планетарную) модель атома. Согласно этой модели вокруг положительного ядра по замкнутым орбитам движутся электроны, образуя электронную оболочку атома, в области с линейными размерами порядка 10^-10 м. Заряд ядра равен Zе (Z. - порядковый номер элемента в системе Менделеева, е —.элементарный заряд), размер 10^-15 – 10^-14 м, масса, практически равна массе атома. Так как атомы нейтральны, то заряд ядра равен суммарному заряду электронов, т. е. вокруг ядра должно вращаться Zэлектронов.

Атом водорода и водородоподобные системы – это системы, состоящие из ядра с зарядом Ze и одного электрона (например, ионы He⁺, Li²⁺).

Решение задачи об энергетических уровнях электрона для атома водорода (а также водородоподобных систем: иона гелия Не⁺, двукратно ионизованного лития Li^{+ +} и др.) сводится к задаче о движении электрона в кулоновском поле ядра.

Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Zе (для атома водорода Z =1),

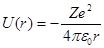, (1) где r – расстояние между электроном и ядром. Графически функция U (r)изображена жирной кривой на рис. 6, неограниченно убывающей (возрастающей.по модулю) при уменьшении r, т. е. при приближении электрона к ядру.

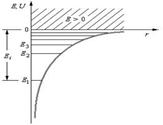
Рис. 6

Состояние электрона в атоме водорода описывается волновой функцией Ψ, удовлетворяющей стационарному уравнению Шредингера, учитывающему значение (1):' 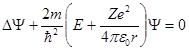, (2)

где m – масса электрона, Е – полная энергия электрона в атоме.

Это так называемое стационарное уравнение Шрёдингера для электрона водородоподобного атома ВДПА.

1. Энергия. В теории дифференциальных уравнений доказывается, что уравнения типа (2) имеют решения, удовлетворяющие требованиям однозначности, конечности и непрерывности волновой функции Ψ, только при собственных значениях энергии 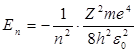(n = 1, 2, 3,…), (3) т. е. для дискретною набора отрицательных значений энергии.

Таким образом, как и в случае «потенциальной ямы» с бесконечно высокими «стенками», решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней. Возможные значения Е₁, Е₂, Е₃,... показаны па рис. 6 в виде горизонтальных прямых. Самый нижний уровень Е₁, отвечающий минимальной возможной энергии, – основной, все остальные (Е_n>E₁, n = 2, 3,…) – возбужденные. При Е < 0 движение электрона является связанным он находится внутри гиперболической «потенциальной ямы». Из рисунка следует, что по мере роста главного квантового числа п энергетические уровни располагаются теснее и при п=∞ Е_∞= 0. При Е > 0 движение электрона является свободным; область непрерывного спектра Е >0 (заштрихована на рис. 6) соответствует ионизованному атому. Энергия ионизации атома водорода равна

E_i = - E₁ = me⁴ / (8h²ε₀²) = 13,55 эВ.

2. Квантовые числа. В квантовой механике доказывается, что уравнению Шредингера (2) удовлетворяют собственные функции 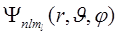, определяемые тремя квантовыми числами: главным п, орбитальным l и магнитным m_l.

Главное квантовое число n, согласно (3), определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения, начиная с единицы: n =1, 2. 3,....

Date: 2015-05-19; view: 520; Нарушение авторских прав