Частица в яме с двумя бесконечно высокими стенками

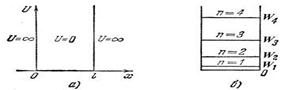
Предположим, что частица может двигаться только вдоль осих. Пусть движение ограничено непроницаемыми для частицы стенками: х= 0 и х= l. Потенциальная энергия U имеет в этом случае следующий вид (рис. 9.2а):

она равна нулю при 0 ≤ х ≤ lи обращается в бесконечность при х<0 их> l. Найдем собственные значения энергии и соответствующие собственные функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме. Поскольку пси-функция зависит только от координаты х, уравнение Шредингера упрощается следующим образом:

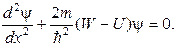(9.3) За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружить частицу, а следовательно, и функция ψза пределами ямы равна нулю. Из условия непрерывности следует, что ψдолжна быть равна нулю и на границы ямы, т. е.

что Ψ(0) = ψ(l) = 0. (9.4) В области, где ψтождественно не равна нулю уравнение (9.3), имеет вид:

.(9.5) Введя обозначение 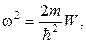(9.6) придем к уравнению, хорошо известному из теории колебаний:

ψ^''+ ω²ψ = 0. Решение такого уравнения имеет вид: Ψ(х) = А sin(ωx+ α). (9.7) Из условия Ψ(0) = 0 получаем Ψ(0) = А sinα= 0, откуда следует, что α должна быть равна нулю. Далее должно выполняться условие: Ψ(l) = А sinωl= 0, что возможно лишь в случае, если ωl= ± nπ (n= 1, 2, 3, …). (9.8)

Из уравнений (9.6) и (9.8) найдем собственные значения энергии частицы: 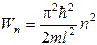(n= 1, 2, 3, …). (9.9)

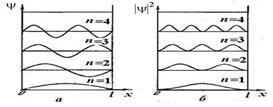
Спектр энергии оказался дискретным. На рис. 9.2б изображена схема энергетических уровней.

Оценим расстояние между соседними уровнями для различных значений массы частицы mи ширины ямы l. Разность энергии двух соседних уровней равна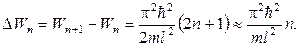

Если взять m порядка массы электрона (9,1∙ 10^{-31 кг), а} l порядка 0,1 м (электрон в сосуде), получим 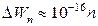эВ. Столь густо расположенные энергетические уровни будут восприниматься как сплошной спектр энергии. Однако совсем иной результат получится для электрона, если область, в которой он движется, будет порядка атомных размеров (~ 10^{-10 м). В этом случае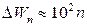} эВ, так что дискретность энергетических уровней будет весьма заметной.

Подставив в (9.7) значение ω, найдем собственные функции задачи:

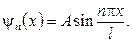Для нахождения А воспользуемся условием нормировки, которое в данном случае запишется следующим образом:

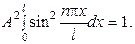В результате получим, что А = 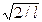.Таким образом, собственные функции имеют вид:

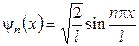(n= 1, 2, 3, …). (9.10)

Графики собственных функций изображены на рис. 9.3а.

На рис.9.3б приведена плотность вероятности обнаружения частицы на различных расстояниях от стенок ямы, равная 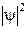.Из графика видно, что, например, в состоянии с n= 2частица не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половине ямы. Отметим, что согласно классическим представлениям все положения частицы в яме равновероятны.

Date: 2015-05-19; view: 725; Нарушение авторских прав