Свободное падение

2.2.1. Определение скорости свободного падения

шарообразных частиц

Как уже говорилось выше, свободным называется падение одиночного тела в неограниченном пространстве или падение массы тел при небольшой объемной концентрации (l < 0,1).

Скорости свободного падения определяются: по теоретическим уравнениям; по эмпирическим и интерполяционным формулам; по графикам и по таблицам, составленным на основе экспериментальных данных.

Скорость свободного падения тела определяется взаимодействием следующих сил: гравитационной, подъемной (архимедовой), гидродинамического (или аэродинамического) сопротивления.

При падении в неподвижной жидкости с начальной нулевой скоростью частица под действием силы тяжести будет постепенно увеличивать скорость падения, одновременно будет расти и сила сопротивления. По истечении некоторого промежутка времени частица приобретет практически постоянную скорость, называемую конечной скоростью падения. С этого момента сила тяжести и подъемная архимедова сила уравновешиваются силой сопротивления: G – А = R _г/а.

Для малых чисел Рейнольдса (Re < 1, ламинарная область) скорость падения шаров может быть рассчитана, исходя из того, что сила сопротивления выражается формулой R = 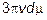, что соответствует зависимости

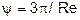. (14)

Выталкивающая сила Архимеда А = V D g (где D – плотность среды, в которую погружено тело).

С учетом того, что сила Архимеда направлена вверх, а сила тяжести вниз, условие достижения телом конечной скорости свободного падения в области малых чисел Рейнольдса можно записать таким образом: G – А = R _г/а; G – А = V r g – V D g = V (r – D) g = (p d ³ / 6)(r – D) g; R _г/а = 3p v ₀ d m, т.е. (p d ³ / 6)(r – D) g = 3p v ₀ d m, отсюда получается формула Стокса (G.G. S toke s):

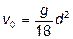
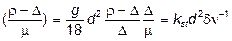, (15)

где коэффициент Стокса; 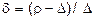– относительная плотность.

Также можно вычислить конечную скорость свободного падения исходя из дифференциального уравнения движения частицы:

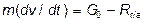; (16)

где 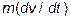– движущая сила; 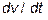– ускорение частицы; m – масса частицы; .

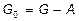От начального момента движения скорость частицы постоянно растет, соответственно растет и силы сопротивления. В некоторый момент времени силы сопротивления становятся равными весу тела в среде. Ускорение же, наоборот, максимально в начальный момент времени движения частицы и постоянно уменьшается, пока не станет равным нулю в тот момент, когда силы сопротивления уравновесят вес тела в среде. Тогда

.

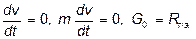Далее вычисление аналогично предыдущему.

Для частиц промежуточного размера (1 < Re < 1000) А.Алленом (A.Allen) экспериментально была установлена формула сопротивления

R _г/а = ;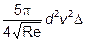

при этом .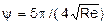

Поскольку 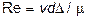, , 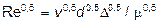по аналогии с вышеизложенным (при достижении конечной скорости свободного падения сила тяжести уравновешивается силами сопротивления) можно записать G – А = R _г/а;

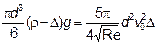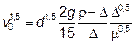; ; или

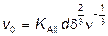(17)

где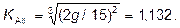

Реально формула Аллена (17) «работает» достаточно надежно лишь при 30 < Re < 300.

Достаточно хорошее приближение к экспериментальным данным для 0,1 < Re < 5000 дает формула, предложенная М.Я.Антонычевым и Ф.И.Нагирняком:

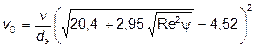. (18)

Ошибка в определении скорости по формуле (18) не превышает 9 %.

При падении крупных частиц (Re > 3000) коэффициент сопротивления – приблизительно постоянная величина (y» p/16). По аналогии с вышеизложенным выведем формулу Ньютона – Риттенгера (I.Newton, P.R.Rittinger). Поскольку G – А = R _г/а; , ,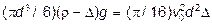

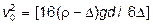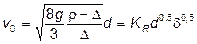, (19)

где K_R – коэффициент Риттенгера.

Интерполяционные формулы для расчета скорости падения сферических частиц получены, как правило, на основании аппроксимации кривой Релея. Наиболее простым способом аппроксимации является разделение кривой на ряд участков, в каждом из которых зависимость между y и Re приближенно заменяется линейной.

Обобщающая формула имеет следующий вид:

v ₀ = 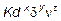, (20)

где K – коэффициент Стокса, Аллена и Риттенгера соответственно для мелких, средних и крупных частиц; 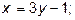y равно 0,5; 2/3 и 1 соответственно для крупных, промежуточных и мелких частиц; .

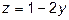Для определения вида частной формулы, которую следует применить в том или ином случае, необходимо знать число Рейнольдса, зависящее, в свою очередь, от искомой скорости. П.В.Лященко предложил использовать безразмерные параметры 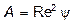и 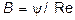. Первый параметр Лященко выводится так: ; ; ; ;

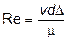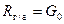
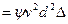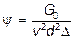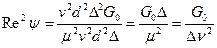
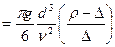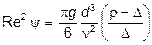. (21)

Для определения гидравлического диаметра (размер частицы, вычисляемый косвенным образом по известной конечной скорости свободного падения) широко используется второй параметр Лященко:

;

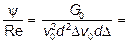
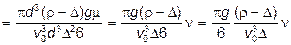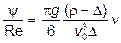. (22)

Первый и второй параметры Лященко используются для отнесения частиц к тому или иному диапазону по крупности, что позволяет использовать ту или иную частную формулу для расчета конечной скорости свободного падения (или размера частицы по известной конечной скорости падения).

Порядок расчета скорости следующий: вычисляем 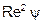по формуле (21); выбираем частную формулу и рассчитываем скорость. Аналогично для расчета гидравлического диаметра вычисляем 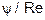по формуле (22), выбираем формулу и вычисляем диаметр. Коэффициент вязкости зависит от температуры и определяется, например, по справочнику [1, с.148].

Рис.4. Диаграмма Лященко

Также для расчета скорости может быть применен графический метод Лященко – Шиллера – Наумана: по формуле (21) рассчитывают первый параметр Лященко 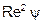. Пользуясь графиком – диаграммой Лященко 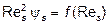(рис.4, для шаров нижняя линия), по найденному значению 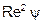определяют Re и по нему, используя формулу (13), вычисляют скорость: .

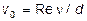2.2.2. Скорость свободного падения тел

правильной несферической формы

Для тел правильной геометрической формы (куб, тетраэдр, октаэдр и др.) имеется определенная зависимость между характерным размером тела, а также коэффициентом сферичности и скоростью падения. За характерный размер для таких тел принимают или диаметр равновеликого по объему шара d _э, или диаметр шара, поверхность которого равна поверхности тела, d_s.

Форма тела характеризуется коэффициентом сферичности [см. формулу (4)]. Причем коэффициент сферичности легко определяется, так как объем и поверхность тела правильной формы достаточно легко вычислить.

Зависимость коэффициента сопротивления y _s (при выборе в качестве характерного размера d_s) от числа Рейнольдса 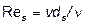для тел различной формы приведена на рис.3, а зависимость 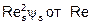– на рис.4. При этом 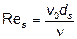; ; 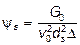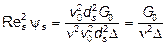Þ

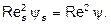(23)

Для всех тел, за исключением дисков, при числах Re < 20 зависимости = f (Re _s) выражаются одной кривой, в то время как при больших значениях Re _s каждому значению коэффициента сферичности соответствует своя линия, удаление которой от оси Re _s увеличивается с уменьшением c (рис.3).

Для определения конечной скорости частиц правильной геометрической формы предложена формула

v _{0 s} = Pv ₀, (24)

где P – коэффициент, зависящий от формы; v ₀ – скорость падения шара, эквивалентного телу по объему.

Для приближенных расчетов при 0,25 < c < 1 можно рекомендовать эмпирические зависимости: при Re _s < 20 (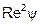 < 350) и Re _s > 500 ( 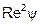> N) соответственно

Р = Р ₁ = 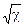(25)

и

Р = Р ₁ = . (26)

Значение N, зависящее от коэффициента сферичности, изменяясь от 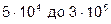, определяется по графику (рис.4). Зависимость коэффициента Р ₁ и Р ₂ от c можно определять либо по графику, либо по таблице (см., например, [1, с.151 и 152]).

Для промежуточных значений 20 < Re _s < 500 (350 < 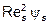< N) скорость падения тел следует определять графическим методом.

Графический метод определения скорости падения тел правильной несферической формы аналогичен применяемому для шаров. Рассчитывают параметр 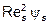[см. формулу (23)]. По его значению с помощью графика (рис.4) для заданной формы находят значение Re _s, после чего искомая скорость определяется по формуле

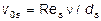. (27)

Таким образом, алгоритм вычисления конечной скорости падения тел правильной несферической формы следующий: определяют 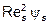, выбирают формулу для расчета (при 350 < 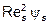< N используют графический метод), рассчитывают скорость.

Для нахождения эквивалентного диаметра частицы по заданной конечной скорости падения можно пользоваться, как и для шаров, графиком, причем значение второго параметра Лященко рассчитывают по формуле

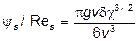. (28)

2.2.3. Скорость свободного падения частиц

неправильной геометрической формы

Для частиц неправильной формы (частицы минералов) четких зависимостей между коэффициентом сопротивления, числом Рейнольдса и коэффициентом сферичности не установлено. Отличие по форме наблюдается не только между частицами разных минералов, но и между частицами одних и тех же минералов. Поэтому под скоростью свободного падения частиц определенной крупности (узкого класса крупности) следует понимать среднюю скорость (например, из 100 замеров). Скорости же отдельных частиц этого класса могут существенно (иногда в несколько раз) отличаться от средней.

За размер частицы принимают средний (среднеарифметический) размер отверстий двух смежных сит d _ср, а в некоторых случаях эквивалентный диаметр шара d _э. Указанные величины для большинства минералов (за исключением имеющих пластинчатую форму) связаны эмпирической зависимостью d _э = (1,05¸1,1) d _ср.

Скорость свободного падения минеральных зерен можно приближенно рассчитать по формулам (24), (25), (26). Основная трудность при их применении состоит в правильном определении коэффициента сферичности.

Для промежуточных значений (20 < Re _s < 500) формулы (25), (26) не применимы, коэффициент Р в формуле (24) следует определять по экспериментальным данным (см., например, [1, с.153]). Приближенно для этой области Р» c.

Обобщающая формула конечной скорости падения (20) для тел любой формы перепишется в таком виде:

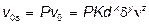, (29)

где .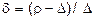

Самым простым способом приближенного определения скорости свободного падения частиц неправильной формы является табличный. Зная минерал и его крупность по таблицам (см., например, [1, с.154, 155]) приближенно определяют скорость его падения.

2.2.4. Равнопадаемость тел при свободном падении

Равнопадающими телами в общем случае называются тела разной крупности, плотности и формы, имеющие одинаковую конечную скорость свободного падения. Так, например, зерно кварца диаметром 4 мм и плотностью 2650 кг/м³ имеет такую же скорость падения, как и зерно галенита диаметром 1 мм и плотностью 7500 кг/м³.

Равнопадаемость приводит к тому, что в один и тот же продукт могут попадать зерна разных минералов (при обогащении), а это ухудшает результаты разделения, либо при классификации в одноименные продукты будут попадать и мелкие, и крупные частицы.

Отношение эквивалентных диаметров равнопадающих тел (более легкого – d _эл к более тяжелому – d _эт) называют коэффициентом равнопадаемости и обозначают 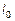(индекс «0» означает свободное падение):

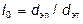, l ₀ > 1. (30)

Для рассматриваемого примера l ₀ = 4.

С целью уменьшения количества равнопадающих зерен перед обогащением стремятся предварительно классифицировать материал по шкале классификации с модулем, равным коэффициенту равнопадаемости.

Если в расчетах коэффициента равнопадаемости использовать уравнение скоростей зерен различной крупности при различных режимах движения (15), (17)-(19), (24)-(26) либо обобщающую формулу (29), то можно получить частные формулы для определения коэффициента равнопадаемости: в области Стокса

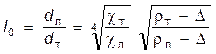; (31)

для частиц с одинаковой формой

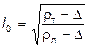; (32)

в области значений Риттингера

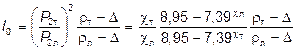; (33)

для частиц с одинаковой формой

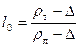. (34)

Здесь в индексах «л» и «т» обозначают соответственно легкую и тяжелую частицу.

Алгоритм вычисления коэффициента равнопадаемости по частным формулам следующий: вычисление второго параметра Лященко; выбор по его значению частной формулы; вычисление коэффициента равнопадаемости.

2.2.5. Движение зерен в центробежном поле

В криволинейных потоках (гидроциклоны, центрифуги) основной движущей силой является сила инерции С, появляющаяся за счет действия центростремительного ускорения. Естественно, силу тяжести G ₀ никто не отменял, и она также продолжает действовать на тело. Тогда 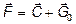. Необходимо учесть также силы сопротивления.

Отношение силы инерции к весу тела в среде (разность между силой тяжести и выталкивающей архимедовой силой) называется фактором разделения, Fr = C / G ₀. Тогда

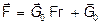. (35)

В центробежных гравитационных аппаратах фактор разделения составляет десятки и сотни единиц, поэтому весом тела в среде можно пренебречь.

Скорость движения частиц во вращающихся (криволинейных) потоках в направлении, перпендикулярном оси вращения, может быть определена по вышеприведенным уравнениям или графическими методами, при условии замены ускорения при свободном падении на центростремительное ускорение (замены веса тела в среде на силу инерции).

Аналогично в центробежном поле конечная скорость достигается, когда движущая сила уравновешивается силами сопротивления:

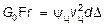. (36)

Для мелких частиц G ₀ F r = 3p v _ц d m, после преобразования имеем

v _ц = v ₀Fr. (37)

Для крупных частиц 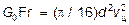, или

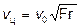. (38)

Для промежуточных частиц определение необходимо вести через 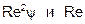. При этом

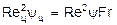. (39)

Очевидно, что скорость движения в центробежном поле для частицы выше, чем ее скорость в гравитационном поле, на величину, пропорциональную фактору разделения. Особенно это сказывается на мелких частицах, поскольку их скорость увеличивается в фактор разделения раз [см. формулу (41)]. Таким образом, мелкая частица в центробежном поле может вести себя аналогично крупной в гравитационном. Поэтому центробежные процессы часто применяют для мелких частиц.

Date: 2015-05-18; view: 1303; Нарушение авторских прав