Гравитационного обогащения

В качестве сред обогащения используют воду, воздух, тяжелые суспензии и жидкости. Среды характеризуются следующими реологическими параметрами: плотностью, вязкостью, предельным сопротивлением сдвигу, устойчивостью.

Плотность среды – отношение массы среды к занимаемому ею объему.

Вязкость – в общем случае, это способность жидкости оказывать сопротивление усилиям, вызывающим относительное перемещение ее частиц. (Когда движение среды прекращается, исчезают и силы внутреннего трения.) Вязкость характеризуют коэффициент динамической вязкости m, коэффициент кинематической вязкости n, напряжение сдвига t.

За единицу вязкости (коэффициент динамической вязкости m) в системе СГС принимают вязкость среды, в которой для поддержания градиента скорости 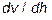= 1 см/с (где 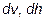– соответственно скорость и расстояние между осями двух элементарных слоев) двух элементарных слоев, расположенных на расстоянии 1 см, на каждый квадратный сантиметр должна действовать сила, равная 1 дин. Единица вязкости в СГС – пуаз (П), 1П = 1 дин×с/см², а в СИ – паскаль-секунда (Па×с).

При гидравлических расчетах часто пользуются кинематическим коэффициентом вязкости – n, представляющим отношение динамического коэффициента вязкости к плотности среды: n = m/D. Коэффициент называется кинематическим вследствие того, что его размерность содержит в себе только кинематические элементы – длину и время.

При увеличении температуры вязкость воды и гидравлической суспензии увеличивается, а вязкость воздуха – уменьшается.

Сила, с которой среда сопротивляется (сила трения),

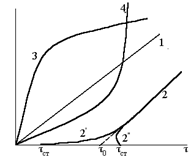
Рис.1. Типы жидких сред

F = 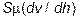, (6)

где S – площадь соприкосновения двух элементарных слоев, 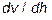– градиент скорости.

В результате внутреннего трения в вязких средах возникают касательные напряжения, которые определяются путем деления силы внутреннего трения на площадь соприкасающихся слоев:

, (7)

т.е. напряжение сдвига t пропорционально градиенту скорости. В этом случае любое малое напряжение сдвига создает градиент скорости, иными словами, приводит жидкость в движение. Такая жидкость называется ньютоновской (кривая 1 на рис.1). Зависимость 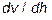от t имеет линейный характер.

Кроме ньютоновских жидкостей существуют и неньтоновские жидкие среды, для которых выражение (7) не справедливо. Они подразделяются на вязко- и псевдопластические среды и дилатансионную систему.

В вязкопластических средах взаимодействие между частицами приводит к их самопроизвольному сцеплению и образованию либо непрерывной структуры, либо отдельных агрегатов. Эти среды характеризуются некоторым предельным (статическим) напряжением сдвига t_ст, после преодоления которого среда начинает течь (кривая 2 на рис.1). Для вязкопластических сред зависимость между напряжением сдвига и градиентом скорости подчиняется закону Шведова – Бингама:

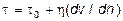, (8)

где h – коэффициент структурной вязкости.

Динамическое напряжение сдвига t₀, в отличие от статического t_ст, представляет собой напряжение, необходимое для разрушения структуры в текущей среде. Соотношение между t_ст и t₀ определяется упругостью среды. Для упругих систем t_ст > t₀ (кривая 2¢¢), а для систем с преобладающими пластическими свойствами t_ст < t₀ кривая 2¢).

Псевдопластические среды не подчиняются закону Ньютона, но и не обладают предельным напряжением сдвига (кривая 3 на рис.1). Для них при достаточно малых значениях напряжения сдвига приблизительно справедливо уравнение (7). По мере увеличения напряжения сдвига кажущаяся вязкость (отношение напряжения сдвига к градиенту скорости) среды уменьшается. Это объясняется тем, что частицы подобных сред имеют палочкообразную форму. При низких градиентах скорости ориентация частиц хаотическая, при увеличении градиента скорости ориентация частиц изменяется в направлении течения потока, вследствие чего и уменьшается кажущаяся вязкость среды.

В дилатансионной системе с увеличением напряжения сдвига кажущаяся вязкость постоянно растет. При достаточно больших напряжениях сдвига градиент скорости остается постоянным (кривая 4 на рис.1). Указанное явление наблюдается в концентрированных суспензиях (l > 42 %).

Помимо указанных, имеются вязкоупругие среды, обладающие одновременно свойствами текучести и упругости.

Тяжелые суспензии, применяемые в практике обогащения, делятся на две основные группы – бесструктурные и структурные. В бесструктурных взаимодействие между частицами утяжелителя отсутствует (малое содержание твердого, добавка пептизаторов), по реологическим свойствам такие суспензии приближаются к ньютоновским жидкостям. В структурных частицы утяжелителя взаимодействуют друг с другом; по реологическим свойствам они приближаются к вязкопластичным системам.

Устойчивость суспензий характеризуется скоростью осаждения твердой фазы. Очевидно, чем крупнее частицы твердой фазы, тем быстрее они осаждаются.

Date: 2015-05-18; view: 446; Нарушение авторских прав