Стесненное падение частиц

2.3.1. Общие положения

Стесненное падение – это падение единичного тела в ограниченном пространстве среды или падение массы тел при достаточно большой объемной концентрации твердого (l > 0,1).

Стесненность падения вызывается наличием стенок аппарата и соседних частиц.

Стесненное движение частиц кроме гравитационных процессов имеет место в ряде процессов химической технологии, при транспортировке пульп по трубам и промывке песчаных фильтров. Движение частиц в узких трубах встречается в некоторых образцах измерительных приборов.

Ввиду сложности стесненное падение изучалось в основном экспериментально. При этом вместо падения частиц исследовалось обычно их взвешивание (от слова взвесь) потоком жидкости. Возможность такой обратимости доказана опытами.

При стесненном падении на отдельную частицу будут действовать те же силы, что и при свободном: гравитационная, подъемная, гидродинамические силы сопротивления (равнодействующая сил трения и давления), силы механического сопротивления, возникающие за счет взаимного столкновения частиц друг с другом, трения частиц друг о друга и стенки аппарата.

Скорость частиц при стесненном падении будет меньше скорости их свободного падения. Чем меньше расстояние между частицами, т.е. чем больше их объемная концентрация, тем меньше будет скорость стесненного падения.

Параметром, характеризующим состояние взвешенного слоя (падающего слоя), является коэффициент разрыхления (пористость слоя) – объемное содержание жидкой фазы в слое:

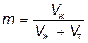, (40)

где V _ж и V _т – объем соответственно жидкой и твердой части слоя.

Объемная концентрация твердого l, вычисляемая по формуле

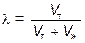, (41)

связана с пористостью следующим соотношением:

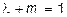. (42)

2.3.2. Частные случаи стесненного падения

Можно выделить четыре вида стесненного падения (рис.5): 1) одиночного тела в однородной среде, ограниченной стенками; 2) массы однородных тел (одинаковой крупности, плотности, формы); 3) отдельных крупных зерен в массе окружающих мелких; 4) массовое падение разнородных зерен.

Лучше всего изучены первый и второй случаи, хуже третий, еще хуже четвертый. Это связано с тем, что виды падения от первого к четвертому становятся все более сложными для изучения.

1. Падение одиночного тела в однородной среде, ограниченной стенками. С некоторым приближением движение частиц в узких трубках можно рассматривать как прообраз стесненного группового движения частиц. Таким путем Монро была получена первая формула для определения скорости стесненного падения. Последующими работами было установлено, что закономерности падения частиц в узких трубках применимы лишь для качественного описания стесненного падения и не дают достаточно точных количественных зависимостей.

Экспериментальное измерение скорости в этом случае производится путем определения скорости восходящего потока v _а взвешивающего частицу, тогда скорость стесненного падения v _ст = v _а,

Скорость можно определить как путь Н, проходимый частицей за определенное время t: v _ст = H / t. Начало и конец отсчета времени движения тела можно фиксировать визуально. Для повышения точности измерений применяют электромагнитную, радиоактивную фиксацию, особенно в непрозрачных средах.

Для расчета скорости падения единичного шара в трубке предложен ряд формул, в которых скорость стесненного падения вычисляется как скорость свободного, умноженная на некий коэффициент, зависящий от 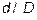. Например, формула Монро

,

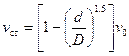где d – диаметр зерна, D – диаметр трубы.

Формула пригодна при 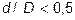. Предложены и другие формулы, отличающиеся главным образом коэффициентом.

2. Падение массы однородных тел. Экспериментально скорость падения массы однородных тел определяют как скорость потока, в котором взвешен определенный объем частиц (при l = const). При этом 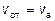. Скорость потока определяют как отношение объема взвешивающей среды (или взвеси) Q, проходящей в единицу времени через сечение S, ограничивающее пространство движения: .

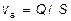Для определения скоростей стесненного падения однородных частиц предложены две основные группы формул: 1) формулы, основанные на рассмотрении массы падающих зерен как фильтрационной среды, через которую жидкость протекает в вертикальном направлении снизу вверх; 2) формулы, основанные на рассмотрении падения в жидкости отдельной частицы, находящейся в массе других.

Хотя первая концепция имеет более четко выраженный физический смысл, недостатком формул этой группы является ограничение применения небольшими коэффициентами разрыхления (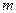 < 0,8), для которых взвешенный слой может рассматриваться как пористая среда.

Для первой группы характерна формула

,

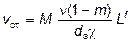где 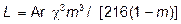; 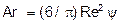– критерий Архимеда; M и f – параметры, зависящие от L.

Из формул второй группы наиболее распространенной является формула Лященко

v _ст = v _св mⁿ, (43)

где v _ст и v _св – скорость соответственно стесненного и свободного падения частиц; n – показатель степени, зависящий от размера, плотности и формы частиц, n можно принимать равным 4,65 при Re < 0,5; 2,39 при Re > 500 и приблизительно 3 при 0,5 < Re < 500; также предложен ряд формул, по которым можно более точно рассчитать показатель степени n.

Подставляя в формулу (43) значение скорости свободного падения из обобщающей формулы конечной скорости свободного падения (29) и учитывая, что 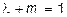, получаем обобщающую формулу конечной скорости стесненного падения

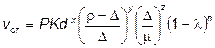. (44)

Все параметры определяются аналогично формулам (20), (29), (43).

Для грубой оценки скорости стесненного падения можно использовать таблицы (см., например, [1, с.157]), в которых приведены значения отношений скоростей стесненного и свободного падения. Также имеются графические методы определения скоростей стесненного падения.

3. Падение отдельных крупных зерен в массе окружающих мелких. Падение отдельных крупных (на несколько порядков крупнее, чем мелкие) зерен в массе окружающих мелких зерен имеет место при обогащении в тяжелых суспензиях. Надо отметить, что в одной и той же суспензии тела одинаковой плотности, но разного размера могут перемещаться по-разному: крупные тела будут тонуть, а мелкие – находиться в равновесии или даже всплывать. Это ограничивает нижний предел крупности частиц, обогащаемых в суспензии.

Экспериментальное определение скоростей падения тел в суспензии может проводиться, например, в вертикальных трубках. Используются неподвижные или движущиеся суспензии. Скорость падения определяется путем фиксации времени прохождения тела через две отметки, для чего можно использовать электромагнитные катушки (тело снабжается магнитным сердечником), радиоактивные счетчики (тело покрывается радиоактивным веществом).

При падении крупных частиц в бесструктурных суспензиях последние по отношению к падающим телам можно рассматривать как жидкость с определенной плотностью и вязкостью, т.е. при Re > 20000 (или 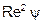> 7×10⁷) скорость падения можно рассчитывать по формуле Ньютона – Риттенгера с учетом плотности суспензии :

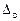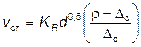. (45)

4. Массовое падение разнородных зерен. Подразумевается падение разнородных, но соизмеримых по размерам частиц, в отличие от предыдущего случая, где падают частицы, размеры которых отличаются на несколько порядков.

Такой вид падения встречается в классификаторах, отсадочных машинах, на концентрационных столах и в ряде других гравитационных аппаратов.

Несмотря на широкое распространение совместное падение разнородных частиц изучено в незначительной степени.

В ряде работ для экспериментального определения скоростей частиц в полидисперсной пульпе применен косвенный метод, основанный на использовании разницы в содержании частиц узких классов в пульпе, находящейся внутри аппарата и выходящей из него.

Качественная картина при движении частиц, соизмеримых по размерам, следующая: при постоянном объемном содержании твердого скорость крупных частиц в присутствии мелких уменьшается по сравнению со скоростью их стесненного падения (при наличии в пульпе частиц только одного крупного класса); наоборот, скорости мелких частиц в присутствии крупных увеличиваются.

2.3.3. Равнопадаемость при стесненном падении

Взвеси, имеющие различные объемные концентрации и состоящие из минеральных частиц, различающихся плотностью, размерами и формой, могут иметь одинаковые скорости падения. Такие взвеси называются равнопадающими.

Коэффициент равнопадаемости при стесненном падении, как и при свободном – это отношение размеров (эквивалентного по объему диаметра) удельно-легкой и удельно-тяжелой частиц.

Из обобщающей формулы (44) получаем коэффициент равнопадаемости для случая стесненного падения в общем виде:

, (46)

где d _эл, d _эт, Р _л, Р _т, r_т, r_л, l_т, l_л – соответственно эквивалентный диаметр легких и тяжелых зерен; коэффициенты, зависящие от формы частиц; плотности тяжелых и легких зерен; объемные содержания твердого для тяжелых и легких зерен; x, y, n определяются, как и в формулах (20) и (43); подставляя их значения, можно получить частные формулы для частиц различной крупности.

Date: 2015-05-18; view: 1753; Нарушение авторских прав