Целочисленный квантовый эффект Холла

В 1980 г. было впервые экспериментально обнаружено, что

полевые зависимости компонент проводимости двумерного

электронного газа кардинально отличаются от предсказаний простой

теории, показанных на рис. 6.1, а. Оказалось, что диссипатив-

ная проводимость 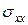действительно обращается в нуль, но не в

отдельных точках, а в целых интервалах магнитных полей, причем

достаточно широких (см. рис. 6.1, б). Еще более поразительным

было поведение 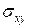, которая в тех же интервалах полей сохраняла

постоянное значение, равное (6.16). Иными словами, холловская

проводимость двумерной системы равнялась величине, не

зависящей ни от параметров образца, ни от магнитного поля, ни от

температуры, а определяемой только значениями фундаментальных

физических констант 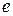и 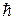. За открытие этого эффекта, названного квантовым эффектом Холла (далее мы будем использовать сокращение КЭХ), К. фон Клитцингу в 1985 г. была присуждена Нобелевская премия.

Заметим, что наблюдать исчезновение 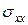и плато на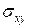

можно не только при изменении магнитного поля, но и при

изменении концентрации носителей путем изменения смещения на

затворе МДП-структуры (именно так впервые был обнаружен КЭХ). Об этом говорит и формула (6.15), из которой следует, что уменьшение концентрации изменяет фактор заполнения 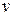таким же образом, как и увеличение магнитного поля.

Физическая модель КЭХ будет описана в следующем разделе,

здесь же мы сделаем еще несколько замечаний относительно

наблюдения и применения этого эффекта. Прежде всего необходимо

иметь в виду, что обращение проводимости 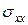в нуль не означает

превращения вещества в идеальный диэлектрик, поскольку

недиагональная компонента 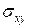при этом отлична от нуля. В условиях

реальных экспериментов обычно через образец пропускают заданный ток

и измеряются напряжения на контактах, т. е. измеряемой величиной является не удельная проводимость 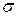, а обратная величина — удельное сопротивление 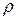. Согласно формулам (6.14) и соотношению (6.16), в областях холловских плато находим

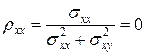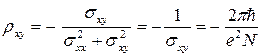, . (6.17)

Таким образом, диагональная компонента сопротивления обращается

в нуль одновременно с диагональной компонентой проводимости, а недиагональная компонента сопротивления (как и проводимости)

принимает квантованные значения, равные комбинации мировых констант.

Исследования показывают, что формулы (6.16), (6.17) являются

точными и не содержат поправок, т. е. с той точностью, с которой

в эксперименте можно измерить сопротивление 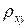, эта величина

равняется 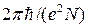. Это означает, что путем высокоточных измерений холловского сопротивления можно определить величину 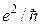. Часто говорится, что КЭХ представляет собой метод прецизионного измерения постоянной тонкой структуры 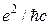. Это связано с тем, что значение скорости света 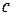хорошо известно из других метрологических измерений с точностью, значительно большей, чем точность измерений е и 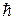как в КЭХ, так и с помощью других методов.

Помимо измерений мировых констант, КЭХ получил и другое

применение в метрологии. Величина 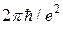, определяемая из

КЭХ, имеет размерность сопротивления и численное значение

~25813 Ом. Поэтому структуру с хорошо выраженными плато

КЭХ можно использовать в качестве эталона сопротивления.

Date: 2015-05-18; view: 615; Нарушение авторских прав