Двумерных систем в магнитном поле

При рассмотрении свойств двумерных систем в квантующих

магнитных полях первое, что необходимо сделать, — это определить энергетический спектр системы путем решения уравнения

Шредингера, что было сделано в предыдущем разделе.

Прежде всего заметим, что в зависимости от ориентации магнитного поля относительно плоскости двумерного слоя могут реализоваться два случая, ответы для которых качественно различны. Если 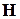лежит в плоскости слоя, то основным результатом будет увеличение энергий квантово-размерных уровней 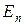за счет дополнительного ограничения движения носителей магнитным полем. Это упрощает наблюдение ряда эффектов, так как позволяет легко менять в эксперименте энергии уровней, что во всех структурах, за исключением МДП-транзисторов, в отсутствие магнитного поля является весьма непростой задачей. Происходит также некоторое

увеличение эффективной массы, описывающей свободное движение в плоскости слоя. В целом можно сказать, что параллельное магнитное поле сохраняет качественный характер энергетического спектра и плотности состояний, хотя и меняет количественно его параметры 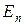и m. Принципиально новых эффектов здесь не ожидается, и мы не будем далее обсуждать случай параллельного поля.

Ситуация, когда магнитное поле ориентировано по нормали к

слою (вдоль оси z), значительно более интересна. Хорошо

известно, что классические траектории частиц в плоскости,

перпендикулярной магнитному полю, представляют собой окружности. В

квантовой механике такое периодическое вращение отвечает

системе эквидистантных дискретных уровней Ландау:

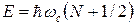, N=0, 1, 2, … (6.1)

Формула (6.1) записана без учета спина.

В массивных трехмерных полупроводниках или металлах к

спектру (6.1) добавляется, как мы видели, еще непрерывный квадратичный спектр 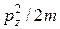, связанный с движением вдоль поля, поэтому суммарная

плотность состояний отлична от нуля при любой энергии, превос-

превосходящей . Однако в двумерных системах движение по

оси z квантовано, так что полный спектр представляет собой сумму

(6.1) и энергий квантово-размерных уровней и, таким образом, является

чисто дискретным. Удивительным является то, что чисто дискретный

спектр обычно характерен для микроскопических объектов

(атомы, квантовые точки и др.). Здесь же мы имеем дело с

макроскопической системой.

В дальнейшем мы ограничимся рассмотрением двумерной

системы с одним заполненным квантово-размерным уровнем

(необходимые критерии этого приведены ранее). Если энергию

этого уровня 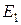выбрать за начало отсчета, то формула (6.1) будет

описывать полный энергетический спектр системы, а не только

его часть, связанную с движением в плоскости ху.

Энергетический спектр (6.1) является сильно вырожденным,

т. е. каждому уровню Ландау соответствует не одно, а много

электронных состояний. Физически природа вырождения достаточно

понятна: в плоскости ху система однородна, что означает, что

состояния, отличающиеся друг от друга лишь положением центра

электронной орбиты, должны иметь одну и ту же энергию.

Простые расчеты показывают, что кратность вырождения

(число различных состояний с одинаковой энергией) в расчете на

единицу площади двумерной структуры равна, согласно формуле (19) предыдущего раздела

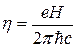. (6.2)

Дискретному электронному спектру (6.1) соответствует плотность состояний в виде совокупности резких пиков, в идеальном случае дельта-функций:

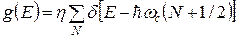. (6.3)

В реальных структурах за счет рассеяния носителей и неоднородного потенциала заряженных примесей дельта-функции будут размываться

в пики с конечной шириной и высотой. Более подробно этот вопрос будет обсуждаться в разделе 6.4.

До сих пор мы не учитывали спин электрона. Наличие спина

приводит к тому, что каждый уровень Ландау 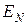двукратно

расщепляется на состояния с энергиями 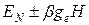, где —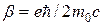

магнетон Бора, a 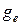— спиновое гиромагнитное отношение

(эффективный g-фактор для электронов). Эта величина, так же как и,

скажем, эффективная масса носителей 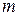, определяется деталями

зонной структуры и может меняться от вещества к веществу во

много раз. Используя известные значения m и 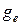для наиболее

распространенных полупроводников, можно показать, что величина

спинового расщепления 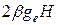, как правило, заметно меньше рас-

расстояния между уровнями Ландау. Существует простой и надежный способ экспериментального разделения эффектов орбитального и спинового квантования, основанный на использовании так называемого наклонного

магнитного поля. Если 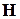отклонено от нормали к двумерному слою

на угол 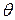, то квантование Ландау (орбитальные эффекты)

определяется лишь нормальной компонентой поля 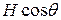, а спиновое

расщепление не зависит от ориентации поля и пропорционально

его полной величине Н.

Date: 2015-05-18; view: 633; Нарушение авторских прав