Кинетические явления в сильных магнитных полях

Чисто дискретный спектр двумерной электронной системы в

перпендикулярном магнитном поле приводит к существенной

модификации ее гальваномагнитных свойств по сравнению с

трехмерным случаем. Отсутствие третьей степени свободы

(свободного движения вдоль поля) приводит к тому, что вероятность

упругого рассеяния носителей испытывает гигантские осцилляции с

магнитным полем.

Действительно, представим себе, что напряженность магнитного

поля Н в точности равна

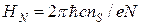(N = 1, 2,...).

Тогда при низких температурах все 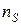электронов, находившиеся в двумерном электронном газе на единицу его площади, полностью заполняют N подуровней Ландау — какие-либо свободные места на них

отсутствуют.

В самом деле, при полном заполнении уровня Ландау кратность вырождения (6.2) – это число электронов на нем. Если рассматривается уровней Ландау 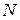и все они заполнены, то

.

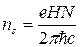Отсюда и получается формула для .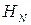

При полном заполнении 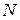уровней Ландау в силу принципа Паули электронных переходов внутри уровней нет. При упругом рассеянии невозможны также переходы на свободные состояния вышележащих уровней, так как это требует дополнительной энергии. Поэтому процессы

рассеяния, представляющие собой переходы из одного состояния в

другое под действием рассеивающего потенциала, в указанных

условиях невозможны.

Чтобы понять, к каким следствиям может привести влияние

магнитных полей на процессы рассеяния, рассмотрим кратко

классическую картину проводимости в сильном магнитном поле. Пусть

магнитное поле 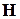направлено по оси z, а тянущее электрическое

поле 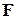— по оси х. Пусть скорость направленного движения

электрона описывается вектором 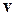. Тогда сила, действующая на него со

стороны полей (сила Лоренца), равна 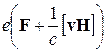. Рассеяние носителей

можно феноменологически рассматривать как эффективную силу тре-

трения, пропорциональную скорости и направленную навстречу ей:

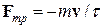(где 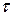— время релаксации). В постоянных полях

дрейфовая скорость электрона постоянна, следовательно,

сумма действующих на него сил равна нулю:

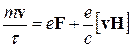. (6.4)

Расписывая уравнение (6.4) по компонентам и определяя из него

компоненты скорост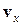и и 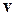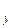, получаем:

,

,

;

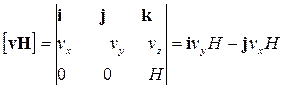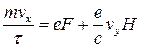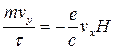Разрешая полученную выше систему алгебраических уравнений относительно 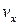и , находим

,

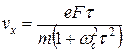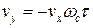. (6.5)

Если 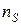— концентрация двумерных электронов, то величина

e 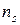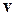представляет собой линейную (в расчете на единицу длины)

плотность тока 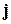. Поскольку связь между векторами F и j дается

тензором проводимости 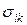, то из (6.5) сразу имеем выражения для

диагональной (диссипативной) 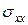и недиагональной (холловской)

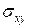компонент проводимости:

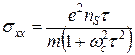, (6.6)

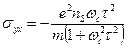. (6.7)

Пусть поле 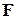направлено теперь по оси OY. Теперь из (6.4) имеем

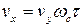, (6.8)

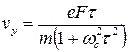. (6.9)

Теперь находим

.

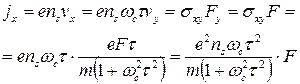Отсюда получается выражение для 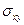. Пусть поле направлено по оси OX.

Имеем

Отсюда вытекает выражение (6.6). Если рассмотреть случай поля 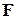, направленного по оси OX, то,повторяя предыдущие рассуждения, легко найти

.

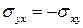Перепишем соотношение 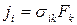(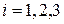, по 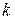подразумевается суммирование от 1 до 3) в матричной форме

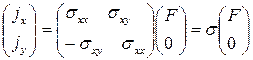. (6.10)

Обозначим через 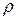матрицу сопротивления. Имеем

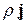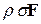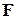= = = , . (6.11)

Обратная матрица находится по обычным правилам

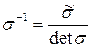. (6.12)

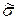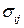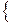
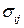
Здесь - присоединенная матрица, полученная транспонированием из матрицы, составленной из алгебраических дополнений к элементам . Напомним, что алгебраическое дополнение к элементу произвольной матрицы 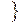- определитель, который получается после вычеркивания 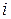-той строки и 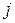-того столбца, умноженный на 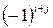. Очевидно, в нашем случае

.

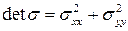Далее имеем

. (6.13)

Отсюда находим

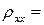
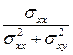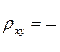
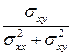, . (6.14)

Из выражений (6.6) и (6.7) видно, что в сильных магнитных полях (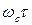 >>1) диссипативная проводимость 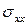пропорциональна вероятности рассеяния 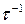, а холловская проводимость не зависит от рассеяния.

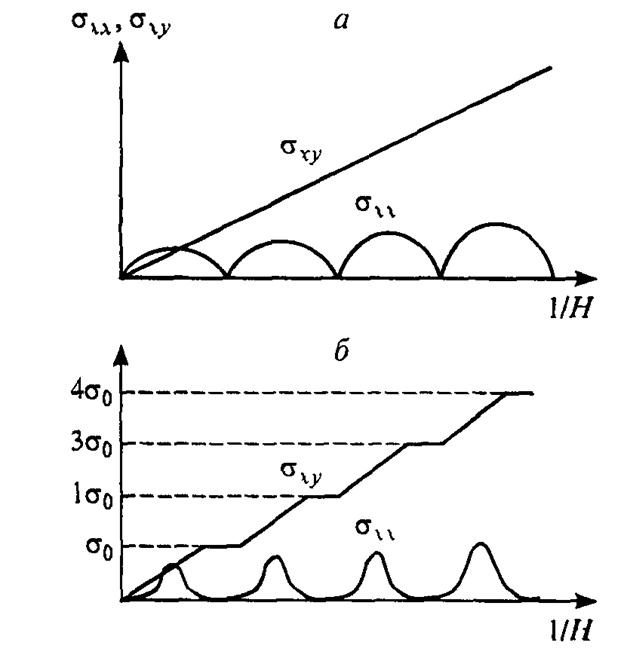
Рис. 6.1. Полевые зависимост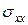и и 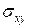в сильных магнитных полях для

идеального двумерного газа (а) и в реальных экспериментах (б) ().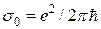

Физически это связано с характером движения

электронов в скрещенных (взаимно перпендикулярных) полях F и Н. Оно представляет собой вращение по круговым орбитам с частотой 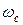при одновременном дрейфе центра орбиты со скоростью 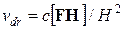. При этом среднее смещение электрона вдоль F отсутствует и появляется

лишь при наличии рассеяния, сбивающего центры орбит.

Обсудим теперь зависимост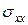и и 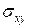от магнитного поля. Как

уже отмечалось, при критических значениях поля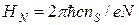

рассеяние отсутствует, т. е. формально 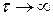. Из (6.6) следует,

что в этих точках 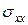должна обращаться в нуль. Что касается ,

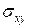то, согласно (6.7), она в координатах 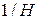должна изменяться

линейно, как это показано на рис. 6.1, а.

Для обсуждения эффектов в сильных магнитных полях очень

удобно пользоваться безразмерным параметром

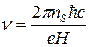, (6.15)

называемым фактором заполнения. Это — число уровней Ландау

(с учетом их спинового расщепления), полностью заполненных

электронами при Т = 0. Критические поля 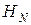соответствуют

целочисленным значениям фактора заполнения.

Весьма интересным оказывается ответ на вопрос, чему равна

холловская проводимость в точках 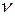= N (N = 1,2, 3,...), где

исчезает диссипативная проводимость, т. е. при 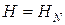. Подставляя

выражение для 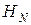в (6.7), где следует также положить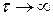

получаем:

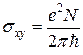. (6.16)

К этому важному выражению, не содержащему ничего, кроме

мировых констант, мы вернемся в следующем разделе.

В самом деле, при выводе (6.16) имеем

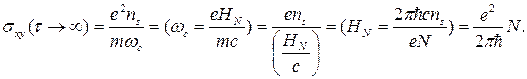
Date: 2015-05-18; view: 830; Нарушение авторских прав