Магнитном поле

Глава. СИЛЬНЫЕ МАГНИТНЫЕ ПОЛЯ И КВАНТОВЫЙ

ЭФФЕКТ ХОЛЛА

Уравнение Шредингера в магнитном поле. Движение в однородном

магнитном поле.

Хорошо известно, что в случае сильных магнитных полей Н,

удовлетворяющих условию 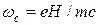>> 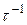и >> ( —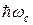

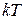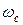циклотронная частота, 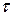— время релаксации), классическое

описание явлений переноса неприменимо и требуется квантово-меха-

нический подход (такие магнитные поля называются квантующими). Это относится и к случаю двумерного электронного газа. Более того, как мы увидим ниже, свойства двумерных систем в квантующих полях еще более разительно, нежели в трехмерном случае, отличаются от предсказаний классической теории.

Как известно, частица со спином обладает и собственным магнитным моментом , причем

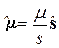, (1)

где 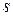- величина спина частицы, а 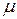- характерная для частицы постоянная. Собственные значения проекции магнитного момента 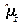равны 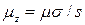. Отсюда видно, что коэффициент 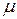(который называют обычно величиной магнитного момента) представляет собой наибольшее возможное значение 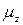, достигаемое при проекции спина 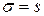. Отношение 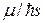- дает отношение собственного магнитного момента частицы к ее собственному механическому моменту, когда оба направлены по оси z. Для электрона

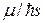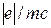= - . Поэтому собственный момент электрона (спи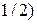н равен

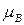- , где

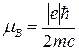=0,927 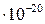эрг/гаусс.

Эту величину называют магнетоном Бора.

В классической теории гамильтониан заряженной частицы в электромагнитом поле имеет вид

,

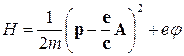где 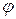-скалярный, 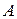-векторный потенциал поля, 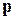- обобщенный импульс частицы. Если частица не обладает спином, то переход к квантовой механике

производится обычным образом: обобщенный импульс надо заменить оператором 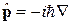, и мы получаем гамильтониан

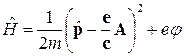. (3)

Собственный магнитный момент частицы непосредственно взаимодействует с магнитным полем. Поэтому необходимо добавить в гамильтониан дополнительный член - 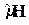, соответствующий энергии магнитного момента в магнитном поле. Поэтому гамильтониан частицы, обладающей спином, имеет вид

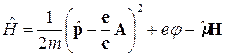. (4)

Волновые функции, на которые действует гамильтониан (4), - спиноры. Волновая функция частицы со спином 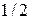имеет две компоненты: и . Двухкомпонентную величину

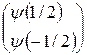
называют спинором. Согласно правилу коммутации оператора импульса с любой функцией координат

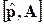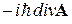= . (5)

В классической механике

.

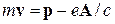В квантовой механике

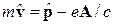. (6)

Для операторов компонент скорости имеют правила коммутации

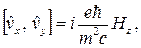
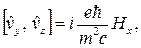
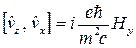. (7)

которые проверяются непосредственным вычислением. В силу (7) частица не может иметь одновременно определенных значений скорости по всем трем направлениям.

Определим уровни энергии частицы в постоянном однородном магнитном поле.

Выберем векторный потенциал однородного поля в форме:

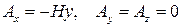. (8)

Ось z выбрана в направлении магнитного поля. В самом деле имели

= .

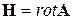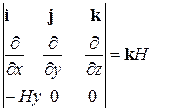Тогда гамильтониан принимает вид

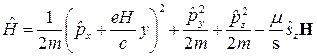. (9)

Оператор 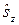коммутирует с гамильтонианом, поскольку последний не содержит операторов других компонент спина. Это значит, что z-проекция спина сохраняется и поэтому 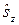можно заменить собственным значением 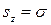. После этого спиновая зависимость волновой функции становится несущественной и 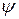в уравнении Шредингера можно понимать как обычную координатную функцию. Для этой функции имеем уравнение

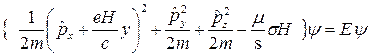. (10)

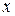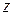Гамильтониан этого уравнения не содержит явно координат и , поэтому с ним коммутативны операторы обобщенного импульса 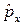и 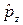, то есть величины 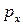и сохраняются. Поэтому ищем 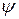в виде

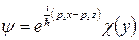. (11)

Поскольку 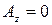, то z-компонента обобщенного импульса совпадает с z-компонентой обычного импульса 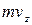. Величины 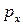и пробегают все значения от 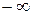до 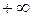. Таким образом, скорость частицы в направлении поля может иметь произвольное значение. Движение вдоль поля «не квантуется».

Далее (11) подставляется в (10). После чего получим

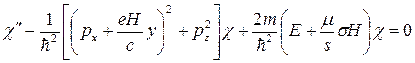. (12)

Введем обозначения

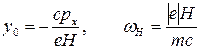. (13)

С учетом данных обозначений перепишем (12) в виде

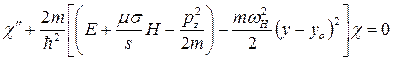. (14)

Уравнение (14) по форме совпадает с уравнением Шредингера для линейного осциллятора, колеблющегося с частотой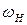

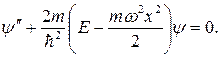
(15)

Поэтому мы можем сразу заключить, что выражение в круглых скобках в (14) может принимать значения 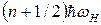, где .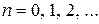

Таким образом, получаем следующее выражение для уровней энергии частицы в однородном магнитном поле

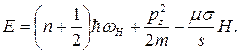(16)

Первый член в (16) дает дискретные значения энергии, отвечающие движению в плоскости, перпендикулярной к полю (уровни Ландау). Так как для электрона 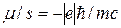, то формула (16) принимает вид

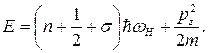(17)

При этом

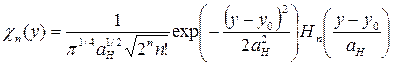, (18)

где .

В классической механике движение частиц в плоскости, перпендикулярной к магнитному полю (плоскость xy), происходит по окружности с неподвижным центром. Сохраняющаяся в квантовом случае величина 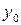соответствует классической y-координате центра окружности. Наряду с ней сохраняется также величина

,

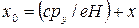так как ее оператор коммутативен с гамильтонианом. Эта величина соответствует классической x- координате центра окружности. Однако операторы 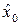и 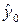не коммутативны друг с другом, так что координаты 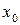и

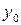не могут одновременно иметь определенных значений.

Поскольку (16), (17) не содержат величины 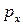, пробегающей непрерывный ряд значений, уровни энергии вырождены с непрерывной кратностью. Кратность вырождения, однако, становится конечной, если движение в плоскости xy ограничено большой, но конечной площадью 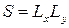. Число различных (теперь дискретных) значений 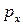в интервале равно

.

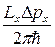Допустимы все значения 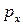, для которых центр орбиты находится внутри 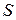. Из условия 0 < 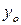< 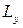имеем (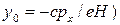

, .

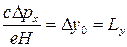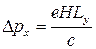Следовательно, число состояний для заданных 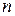и есть

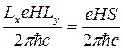. (19)

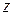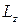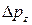Если область движения ограничена также и вдоль оси длиной , то число возможных значений в интервале есть 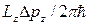и число состояний в этом интервале есть

(20)

Для электрона имеет место еще дополнительное вырождение: уровни энергии совпадают для состояний с квантовыми числам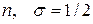и и .

Date: 2015-05-18; view: 637; Нарушение авторских прав