Из свойств (4.6) и (4.9) следует вещественность модуля вектора

Бесконечномерные полные унитарные пространства с конечной нормой для всех векторов называются гильбертовыми пространствами (Г–пространствами). Полнота пространства означает, что оно содержит все необходимые векторы для разложения любого своего вектора в сумму (или интеграл) (4.5).

В Г–пространстве можно выбрать ортогональную систему линейно независимых векторов с единичными модулями

(j_ί,j_ĸ) = δ_ίĸ (4.12)

С помощью условия ортогональности базисных векторов (4.12) в разложении (4.5) легко найти координаты вектора. Для этого достаточно умножить вектор (4.5) слева скалярно на j_ĸ :

(j_ĸ ,y) = Σ (j_ĸ,c_ίj_ί ) = Σ c_ί(j_ĸ,j_ί ) = c_ĸ, (4.13)

т.е. координаты вектора в ортонормированном базисе называются его проекциями. Совокупность проекций вектора даёт исчерпывающую информацию о нём. Следовательно, вектор при известном базисе может быть задан в виде упорядоченной совокупности своих проекций.

Формулу для расчёта скалярного произведения двух векторов через их проекции в ортонормированном базисе получим, используя разложение (4.5), выражение χ = ∑d_ĸj_ĸ и свойства скалярного произведения (4.10):

(y,j) = ∑ ∑c_ί*d_ĸ(j_ί ,j_ĸ) = ∑c_ί*d_ί (4.14)

Норма вектора представляется аналогичной формулой:

(y,y) = ∑c_ί*c_ί . (4.14′)

В выражениях (4.14), (4.14′) бесконечные ряды сходятся к конечным вещественным числам.

В ряде задач квантовой механики используются в качестве базисных такие векторы, норма которых не является конечным числом, т.е. векторы не гильбертова пространства. В таких случаях система базисных векторов оказывается непрерывной и нормированной на δ –функцию Дирака.

4.2. Операторы в линейном векторном пространстве.

Оператор есть символ, выражающий правило, согласно которому каждому вектору y из некоторого множества ставится в соответствие другой вектор j (из этого же или другого множества):

Ây = j (4.15)

Операторы обозначаются большими латинскими буквами со “шляпкой–крышкой” наверху, например, Â, Ĉ, Ĥ, Ŝ, …

В уравнении (4.15) под Â можно подразумевать любую операцию: умножение на координату x (Â = x), дифференцирование по x (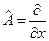), извлечение корня квадратного (Â = Ö) и т.д.

В квантовой механике используются линейные операторы.

А) Линейные самосопряжённые (эрмитовы) операторы.

Оператор Â называют линейным, если он удовлетворяет условию:

Â(с₁y₁ + с₂y₂) = с₁Ây₁ + с₂Ây₂, (4.16)

где с₁ и с₂ – некоторые постоянные комплексные числа.

Символы операторов представляют собою самостоятельные математические объекты, над которыми можно производить ряд математических действий: сложение, умножение, возведение в степень, разложение в степенной ряд.

Оператор Ĉ называется суммой операторов Â и 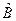, т.е.

Ĉ = Â + 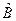, (4.17)

Date: 2015-05-18; view: 481; Нарушение авторских прав