Электростатическое поле

Можно сделать второе упрощающее допущение, заключающееся в том, что мы пренебрегаем нетождественностью пространственно-временной системы О с пространственно-временной системой Q, но принимаем во внимание только внутренние напряжения тел, порождающих поле, и исследуемого тела Р.

Тогда мы имеем:

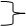U₃ ≠ q

v = q (22)

Это дает f = 0 и e ≠ 0.

В том случае, когда U₁ и U₂ лежат в плоскости, ортогональной к ³Q и являются ортогональными в точном смысле, мы получаем:

U₁ ≡ ¹Q, U₂ ≡ ²Q,

поскольку это означает только, что О находится в состоянии покоя по отношению к телу, порождающему поле.

Это дает:

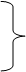U₁ = (1, 0, 0)

U₂ = (0, 1, 0) (23)

U₃ = (ie, e, 1)

v = (0, 0, 1)

Ситуация, когда О не находится в состоянии покоя по отношению к координатам Q, может быть сведена к мгновенному вращению, и ее следует рассматривать, принимая во внимание вторичные эффекты, в частности магнитное поле вращающихся массивных тел.

Из (23) мы имеем:

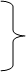d¹q = ∆х¹ + ie∆х³

d²q = ∆х² + e∆х³ (24)

d³q = ∆х³

∆³q = ds sin λ

Исключая ненаблюдаемое ∆х³ и оставляя только члены содержащие e не выше первой степени, получаем

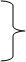d¹q = ∆х¹ + ie ds sin λ

d²q = ∆х² + e ds sin λ (25)

d³q = ds sin λ

Подставляя это в (1), получаем:

ds² cos² λ - 2 ds sinλ e (i∆х¹ + ∆х²) = (∆х¹)² + (∆х²)² (26)

Сохраняя члены с e, не выше первой степени, можно выделить полный квадрат в левой части уравнения (26) и опустить соответствующие квадраты в правой части. Это дает:

[ds cos λ – e tan λ (i∆х¹ + ∆х²)]² = (∆х¹)² + (∆х²)² (27)

Рассматривая момент, когда Р находится в состоянии покоя по отношению к О (т.е. момент начала свободного падения Р), мы имеем:

∆х¹/∆х² = скорость Р / ic = 0 (28)

так что мы можем написать:

ds cos λ = ∆х² (1 + e tan λ) (29)

Сравнивая с Лагранжианом в форме (10), мы имеем:

L = - m_оc² e tan λ (30)

из чего можно видеть, что электростатический потенциал задается формулой:

Ω_c @ m_оc² e tan λ (31)

Последующий анализ включает аппроксимации, допустимость которых выявляется только при детальном анализе в пяти измерениях. Все вышесказанное предназначалось только для того, чтобы помочь читателю увидеть как условия системы координат – объединенные с постулатом псевдожесткости и нечувствительности к вечности – приводят к гравитационному и электромагнитному полям. Уравнения для последнего (включающие пространственные вариации) можно легко вывести только в том случае, когда рассматриваются три измерения пространства.

Отметим, что электростатический потенциал не зависит от измерительной системы О, поскольку угол λ является свойством Р (направление космодезической в многообразии Q), которое не связано с О. Когда λ равен нулю, равно нулю Ω_c. Это интерпретируется как то, что р не заряжено. Поскольку tan λ может быть как положительным, так и отрицательным, заряд может иметь разные знаки, и поле может быть как притягивающим, так и отталкивающим. Таким образом, можно видеть, что свойства электростатического (а для пяти измерений электромагнитного) поля можно вывести из предположений:

(а) Нет взаимодействия между О и Р,

v ≡ ³Q

.

(б) Внутренняя структура Р и тел, порождающих поле должна приниматься во внимание

U₃ ¹ ³Q.

(в) О – М – R является квази-жесткой системой.

(г) О нечувствителен к вечности.

Эти предположения приводят также к закону обратного квадрата силы. Это завершает схему, посредством которой гипотеза приводит к единой теории поля для гравитационных электромагнитных полей и гравитационно-магнитных взаимодействий.

Для более строгого анализа следует обратиться к исходной статье.

Приложение 3 к Главе 15

ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ

ТОЖДЕСТВА И РАЗЛИЧИЯ

Date: 2015-05-18; view: 480; Нарушение авторских прав