Общее выражение для интервала

Для того, чтобы задать область для наблюдателя О, не являющегося локальным наблюдателем, т.е. не прикрепленного жестко к системе О – М – R, мы можем рассмотреть тело Р, движущееся независимо от О. Это "невынужденное свободно падающее тело". Предполагается, что Р не оказывает влияния на поле, т.е. Р обладает пренебрежимо малой массой и зарядом, по сравнению с О и полем, порожденным телом S. Нам нужно получить выражение для интервала ds движения тела Р. По определению, путь Р является космодезической, т.е. прямой линией, как это может установить универсальный наблюдатель Q. Исключая те точки, где ускорения очень велики, путь Р будет очень близок к общему направлению временной актуализации. Это можно выразить требованием, что космодезическая Р составляет угол (½π – λ) с Q, где λ – малый угол.

Теперь из отношений, заданных в уравнениях (3):

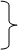d¹q = a∆х¹ - ib∆х² + ie∆х³

d²q = ib∆х¹ + d∆х² + e∆х³ (5)

d³q = -if∆х¹ - f∆х² + ∆х³

Мы имеем в дополнение:

d³q = ds sin λ

Это дает возможность исключить ∆х³, который является интервалом неизмеримым для О вследствие его нечувствительности к вечности. Теперь мы имеем отношение между измерениями, которые делает Q в трех измерениях пространства, времени и вечности, и измерениями, которые делает О в своей и нашей ограниченной и нечувствительной к вечности измерительной системе.

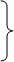d¹q = ieds sinλ + (a – ef) ∆х¹ + (-b + ef)i∆х²

d²q = eds sinλ + (b +ef)i∆х¹ + (-d + ef)∆х² (7)

d³q = - ds sin λ

Подставляя из (7) в (1), получаем требуемое отношение:

ds cos λ – 2ds sin λ [i ∆х¹ (a + b) + ∆х²(d +b)] =

= (∆х¹)²[ 1 + f² –2ef ] + (∆х²)² [1 - f² + 2ef] + 4i∆х¹∆х²ef (8)

Это уравнение дает точность до третьего порядка малости.

Date: 2015-05-18; view: 429; Нарушение авторских прав