Гравитационное поле

Ситуация, в которой внутренними напряжениями тала, которое порождает поле, и исследуемого тела можно пренебречь соответствует отсутствию электрического заряда. Поскольку отсутствие внутренних сил означает, что нет внутренней потенциальной энергии, мы имеем, что U₃ совпадает с ³Q. Это является условием гравитационного поля. Силы возникают в результате несовпадения плоскости пространственно-временных осей с плоскостью, ортогональной к ³Q. Это означает, что v не совпадает с ³Q, но они образуют нуль-угол. Соответственно, мы имеем:

е = 0

f ≠ 0

b, d и f малые и конечные.

Следовательно

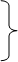U₁ = (a, ib, -if)

U₂ = (-ib, d, -f) (13)

U₃ = (0, 0, 1)

v = (if, f, 1)

где

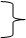a² = 1 + b² + f²

d² = 1 +b² –f² (14)

Из этого следует, что:

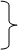d¹q = a∆х¹ - ib∆х²

d²q = ib∆х¹ + d∆х² (15)

и d³q = ds sin λ, как выше

Это позволяет нам записать (1) в форме, которая не содержит ∆х³, а именно:

ds² cos² λ = (a∆х¹ - ib∆х²)² + (ib∆х¹ + d∆х²)² = (∆х¹)²(a² – b²) + (∆х²)²(d² – b²) (16)

Используя (14), имеем:

ds² cos λ = (∆х¹)²(1 + f²) + (∆х²)²(1 – f²) (17)

Отмечая, что ∆х¹ является мнимой (пространство-подобной) координатой и что мы рассматриваем только направление мгновенного ускорения Р, мы можем видеть, что (17) эквивалентно уравнению Шварцшильда, которое корректно определяет функцию f (для полноты обсуждения следует обратиться к цитируемой работе). Интерпретация (17) призывает обратить пристальное внимание на характер действий, выполняемых О при получении данных, соответствующих кажущемуся пути Р в его собственной мгновенной системе координат наблюдения. Следовательно, мы не должны рассматривать общую метрику в смысле потока в теории поля. Универсальная метрика существует только для Q. О не может проводить измерений вне границ его собственной измерительной системы. Он может, следовательно, принимать во внимание только мгновенные направления актуализации и ускорения (т.е. время и пространство).

Уравнение (17) дает результаты измерений О, и ничего больше, в то время как в обычной интерпретации уравнения Шварцшильда метрика имплицитно рассматривается как независимая от существования О. Интерпретация (17) вследствие предположений относительно характера измерительной системы О, делает аппарат обработки полностью релятивистским в истинном смысле слова. Легко можно видеть, что кажущаяся траектория Р, как ее наблюдает О, соответствует во всех отношениях телу, свободно падающему в силовом поле тяготения, включая поправку Эйнштейна к теории Ньютона.

Простой вывод гравитационного потенциала получается, если опустить в поправке Эйнштейна член f²(∆х¹)², и использовать уравнения (10) и (17),

(1 – L/m_оc²)² = 1 – f² – (V¹)²/c² (18)

откуда, L @ m_оc² [1 – (1 - (V¹)²/c² - f²)^½ ] (19)

Сравнивая с классическим Логранжианом:

L = m_оc² [1 – (1 - (V¹)²/c²)^½ ] - Ω_c (20)

имеем: Ω_c @ - ½m_оc² f² (21)

Следовательно, потенциальная энергия любого тела в поле этого типа пропорциональна массе инерции и всегда отрицательна (порождая силу тяготения). Постулат квази-жесткости приводит к закону обратного квадрата для f.

Date: 2015-05-18; view: 400; Нарушение авторских прав