Общие законы природы должны выражаться уравнениями, которые

подходят для всех систем координат, т.е. ковариантны относительно

любой замены переменных.

Первый шаг в разработанной Эйнштейном общей теории относительности заключается в выдвижении определенных предположений о том, как способ проведения измерений в пространстве и времени связан с четырьмя координатами, эти допущения, которые строго обоснованы только в бесконечно малой области, в которой можно пренебречь ускорением, приводят к инвариантному выражению для квадрата линейного элемента.

Следующий шаг заключается в соответствующем предположении о способе, которым можно применять общее выражение к непрямолинейным движениям. Это, в действительности, равносильно установлению определенных условий симметрии, относящихся к тому, как должны выполняться изменения. На третьем шаге происходит переход прямо к законам, относящемся к импульсу и энергии, посредством функции Гамильтона.

В первом сообщении о своей теории Эйнштейн попытался продемонстрировать правдоподобие этих допущений, апеллируя к нашей интуиции, что не может быть привилегированной системы отсчета, соответствующей актуализации некоторого произвольного целого. Он также показал, что его уравнения движения более успешно редуцируют феномены к факту, чем уравнения Ньютона, особенно по отношению к поведению света в гравитационном поле. Здесь мы снова проводим различие между относящимся к феноменам гипотезами и теми альтернативными путями, посредством которых феномены могут быть редуцированы к фактам. Вскоре после того, как Эйнштейн опубликовал свою работу по теории относительности, Уайтхед показал, что уравнения, описывающие наблюдаемые факты можно вывести без особых предположений, сделанных Эйнштейном о том, как способ проведения физических измерений может быть связан с координатами.

Эйнштейн справедливо утверждал, что развитый им математический аппарат тензорного исчисления дал средства для обобщения физических законов материи таким образом, что они могут быть согласованы с общей теорией относительности. Это исключительно яркое достижение, но оно не должно ослеплять нас настолько, чтобы мы стали делать предположения произвольного характера. Сам Эйнштейн утверждал, что общий принцип относительности "сообщает нам о влиянии гравитационного поля на все процессы, не предоставляя в наше распоряжение какой-либо новой гипотезы". Далее он отмечает: "…выходит, что нет необходимости вводить определенные предположения относительно физической природы материи (в более узком смысле). В частности, можно оставить открытым вопрос, дает ли теория электромагнитного поля вместе с теорией гравитационного поля достаточный базис для теории материи, или нет. Общий постулат относительности в принципе не может сказать нам что-либо об этом". В принятой нами терминологии это означает, что общая теория относительности не является гипотезой существования и, следовательно, в общем смысле не приложима к феноменам. Ее история, в продолжение тридцати пяти лет с того момента, как она была впервые сформулирована, полностью подтверждает это заключение. Ожидания, что комбинация электромагнитной теории с теорией гравитационного поля даст адекватную оценку материи, не оправдались. В самом деле, общая тенденция физической науки заключается в отходе от надежды на накопление данных, полученных от более глубокого проникновения в природу физического мира, в пользу символического описания, которое является математически содержательным, даже если не может быть осмыслено физически. Гейзенберг писал в 1952 году: "Следует отметить, что статусы ограниченного и общего принципов относительности весьма различны. Современная физическая теория целиком пропитана влиянием специальной теории относительности, в то время как общая теория относительности остается остроумной и яркой спекуляцией, которая имеет мало значения для прогресса физической науки".

Начиная с 1927 года, многие физики, и в частности Розенфельд и Флинт поддерживали концепцию пятимерного мира, но она не была принята основной массой физиков, несмотря на фундаментальную роль, которую играет пятерка независимых значений координат Е в замечательных исследованиях Эддингтона о происхождении фундаментальных физических постоянных. Однако, Эддингтон рассматривал Е₅ не как независимое направление в геометрическом многообразии, а только как меру локальной кривизны. Отсюда поразительный результат, что Е₅ может быть как действительной, так и мнимой величиной, в соответствии с тем, сколько частиц присутствует, одна или много.

Как и общая теория относительности Эйнштейна, гипотеза Вейля-Дирака-Эддингтона является попыткой втиснуть физические данные в пространственно-временную систему координат, и таким образом она имеет характер, фундаментально отличающийся от теории, предлагаемой в настоящей работе. Эддингтон в теории относительности протонов и электронов, разделяет свою форму тензора Римана-Кристоффеля на кинематическую и электрическую составляющие. В объединении теории относительности и квантовой теории это разделение является основой, на которой строится попытка вывода постоянных М/m и hc/e ², которые, конечно, обе безразмерные. Физики-теоретики мало расположены принимать анализ Эддингтона, несмотря на остроумный статистический аппарат.

Пятимерные теории, направленные в первую очередь на устранение противоречий в волновой механике и квантовой теории развивались Флинтом. В этих теориях пятое измерения связывалось с волновой функцией. Основной целью являлось установление связи матричной механики электронов, протонов и атомных ядер с квантовой теорией, используя гармонические возможности пятого измерения. Эта геометрия является римановой геометрией пространства-времени Эйнштейна.

Имеется также ряд исследований, включающих пятимерные теории, в которых пятому измерению приписывалось определенное физическое значение. Уилсон, определяя пятимерное космическое многообразие, как содержащее траектории всех частиц, описывающих геодезические, распространил вариационный принцип Гамильтона на пять измерений и связал его с распространением материальной волны де Бройля. Это было до тех пор, пока не стали появляться статьи, в которых пятое измерение связывалось с энергией и энтропией. В 1942 году Кальдирола определил пятое измерение в терминах временного и энергетического содержимого системы:

xº₅ = Т/(Е+S)dt

Цель Кальдиролы состоит в том, чтобы вывести мезонное поле из метрики, используя обобщенный пятимерный вектор. Геометрия пятимерного многообразия Кальдиролы является геометрией четырехмерного Риманова пространства, вместе с измерением времени, добавленным в качестве пятого измерения. Предположение, что единую теорию поля можно вывести из пятимерного Евклидова многообразия выдвинули Ван и Чень еще в 1946г. Однако, они строили поля не на основе характера космического многообразия, а вводили гравитационный и электростатический потенциал, как независимые вектора в пятимерном евклидовом пространстве. Они высказали предположение, что если сделать соответствующие допущения относительно природы распределения заряда в пятом измерении Х(5), то можно получить уравнения поля и взаимодействий с частицами. По предположению, пятое измерение должно быть пространство-подобным, но "как импульс, так и скорость частицы в пятом измерении не наблюдаемы, и предполагаются нулевыми". Целью статьи является вывод связываний для мезонной теории.

Джао в 1946г предложил новый путь использования (n+1)-мерного космического многообразия, которое является евклидовым по характеру, но включает в себя n-мерные римановы пространства, соответствующие полю потенциалов. Особой чертой теории Джао является то, что он отождествил физическое существование с математической непроизвольностью. Определение "Непроизвольного математического бытия" возникает из представления об области изменения переменной как о "сосуде" и о функции этой переменной как о "содержимом". Иногда использование пяти измерений следует из предположений a priori о типе функции. Джао можно рассматривать как представителя крайней точки зрения, игнорирующей принцип, что связи подразумевают отношение. Кажется, что он допускает, что определенный вид отношения (математическая непроизвольность) может существовать на своей собственной основе. Очевидно, что эти понятия, хотя и внешне похожи, но, в действительности, совершенно отличны от соответствующих понятий настоящей работы.

В качестве альтернативного подхода к построению космологической модели можно вспомнить подход Вейля, основанный на аффинной геометрии. Вероятно, Шредингер сделал все, что возможно в этом направлении, в исключительно красивой по своей математической общности статье. Целью Шредингера было ввести законы взаимодействия в форме мезонного поля в единую космологическую структуру вместе с гравитацией и электромагнетизмом. Оказывается, что общий подход, предложенный в исследованиях Шредингера, Борна и других физиков, принимавших участие в последние годы в разработке обобщенной теории поля, если его интерпретировать в терминах нашей категориальной схемы, доходит до отрицания того, что гипарксис имеет такой же статус, как время и пространство, и до пренебрежениями детерминирующим условием вечности. Степени свободы, требующиеся для компенсации этого ограничения в системе координат, получаются посредством ослабления условий, накладываемых на допустимые отношения в пространственно-временной системе. Как оказывается в частности, Борн и Шредингер получают свои дополнительные параметры при помощи аргументов, чуждых аффинной космической геометрии.

Другая группа теорий представлена Эйнштейновской "гипотезой бивектора". Процедура заключается в построении системы координат более общей, чем система координат римановой геометрии с единственной функцией кривизны, при помощи замены контравариантного метрического тензора контравариантным бивектором. Это оказывается эквивалентным постулированию аффинной геометрии, в которой метрика вводится как два независимых римановых многообразия. Эта процедура так же открыта для метафизических возражений, как и процедура Шредингера, и в дополнение к этому дает уравнения поля, которые почти невозможно решить.

Обобщая все это, можно сказать, что исследования тридцати последних лет, прошедших с того времени, как Эйнштейн впервые предложил использовать риманову геометрию, не дали результатов, которые могли бы оправдать отход от геометрии специальной теории относительности Минковского.

Дингль предложил подход целиком отличный от этого, в котором он различает два типа времени, одно динамическое, а другое тепловое. Понимая, что термодинамический характер времени полностью отсутствует в схеме общей теории относительности, Дингль пишет: "Следующим шагом к теории поля, очевидно, является отказ от пространственной системы измерения времени механики для тепловой молекулы и принятие новой системы, в которой время измеряется в терминах интервалов некоторой измеримой тепловой величины. Если сделать это, оно само рационализуется в терминах чистой теории поля, и единственная задача по формулировке метрических законов, которая остается физикам, это объединение механики, электромагнетизма и термодинамики в единую теорию поля". Для тех, кто немного знаком с техникой общей теории относительности, я рискну сделать первое и последнее весьма краткое вторжение в математический язык, чтобы сформулировать это более определенно.

"Интервал собственного времени между двумя событиями механики в пространственно-временном континууме в теории Эйнштейна приблизительно задается выражением:

dS² = FdT² - GdS²

где dT и dS малые временной и пространственный интервалы соответственно, а F и G нас не интересуют, кроме того факта, что они включают в себя скорость света. Теперь, опуская для упрощения электромагнетизм, рассмотрим интервал в пространственно-термо-временном континууме, соответствующем предполагаемой теории поля, которая включает механику (релятивистскую, а не ньютоновскую) и термодинамику. Простейшее обобщение, подходящее для иллюстрации, задается формой:

dS² = FdT² - GdS² - KdH²

где dH – выбранный тепловой интервал.

"Этот интервал потенциально способен включать в себя все парадоксы квантовой теории без их парадоксального аспекта. Неопределенность, выраженная принципом Гейзенберга, может являться аналогом неопределенности, в соответствии с точкой зрения общей теории относительности, "сейчас" Ньютоновского времени, и, подобно этой неопределенности, должна будет исчезнуть из собственной меры, вместо того, чтобы оставаться в несовершенной формулировке, как это имеет место в квантовой теории. Следующий парадокс квантовой теории, заключающийся в том, что данные необходимые для определения события, оказываются иногда лежащими в будущем этого события, должен также иметь очевидное объяснение. Они должны лежать не в собственном будущем, а только в координатном будущем – а именно в том, которое получается, когда мы пренебрегаем членом с dH²: это, конечно, только в микроскопических феноменах, где dS и dT настолько малы, что член, обычно пренебрежимый, может стать достаточно значительным для возникновения этого парадокса. "

"Я приношу свои извинения за это погружение в специальный язык. Это не является необходимым для подкрепления общих аргументов, но придает больше ясности для того, кто понимает символизм. Принимая должным образом во внимание факт, что это пока является спекуляцией (поскольку H еще не установлено, а К задается в виде выражения законов теплоты), мы можем видеть здесь, по меньшей мере, представимое направление развития, которое могло бы сохранить все достижения квантовой теории, без обязательных несообразностей, которые их сейчас сопровождают". Видно, что Дингль здесь очень близко подошел к тому различению времени, вечности и гипарксиса, которое делается нами.

Термодинамические различия времени и вечности неявно выражены в работе Фантаппи, который разделяет два космических процесса энтропии и синтропии. Его синтропические феномены не воспроизводимы, интенсивны и не наблюдаемы, и близко приближаются к нашему понятию вечности, как области сохранения потенциальности.

И, наконец, можно сослаться на очень важную работу Подаланского, в которой он попытался объединить теорию поля и квантовую механики при помощи шестимерной геометрии.³¹ Однако, он особо отмечает, что его представление "можно классифицировать как вложенную теорию, поскольку электромагнитная сила имеем характер вынужденных сил" Нечувствительность наблюдателя к вечности и ее связь с деформацией в квази-жесткой системе измерения понимается в смысле "безобидности", означающем, что в наблюдателе не происходит физических изменений при его перемещении в пятом и шестом измерениях. Следует, однако, понимать, что термодинамическое различие между временем и вечностью в теории Подаланского пропущено, как и во всех предшествующих ей теориях.

Этот краткий и по неизбежности неполный обзор достаточен для того, чтобы показать, что математики и физики-теоретики давно признали возможность того, что система координат четырехмерного пространства-времени может оказаться неадекватной. Сделанный шаг может быть обоснован только в том случае, если мы понимаем фундаментальное различие между функцией, бытием и волей. Если существование и определяющие условия каким-либо образом смешиваются, схема представления, которую мы построим, неизбежно окажется абстрактной и конвенциональной. Напротив, если мы обнаружим, что феномены во всем их бесконечном разнообразии можно представить в терминах той или иной геометрии, мы сможем ощутить уверенность в том, что мы приблизились к опыту, а не к некоторой искусственной конструкции нашего собственного ума.

Приложение 2 к Главе 14

ЕДИНАЯ ТЕОРИЯ ПОЛЯ

1. УПРОЩЕННЫЙ МАТЕМАТИЧЕСКИЙ АППАРАТ

Вывод уравнений поля для центрально направленных сил в пятимерном многообразии дан в другой работе. Упрощенный анализ можно получить, рассматривая пространство, время и вечность, каждое как одно измерение. Это эквивалентно рассмотрению только мгновенного направления силы в пространстве. Это позволяет нам использовать в качестве ссылочной системы координат трехмерное многообразие с одной мнимой осью ¹Q (пространство-подобной) и двумя действительными (время и вечностно-подобной) осями ²Q и ³Q. Они выбираются взаимноортогональными в псевдоевклидовом многообразии. Считая мнимой осью d¹q, мы задаем интервал посредством выражения:

Ds² = (d¹q)² + (d²q)² +(d³q)² (1)

где d¹q, d²q, d³q являются перемещениями вдоль осей ¹Q, ²Q, ³Q соответственно. Наблюдения, необходимые для измерения таких интервалов, могут быть сделаны, вообще говоря, только универсальным наблюдателем Q, который не ограничен отдельной областью вечности. Чтобы связать интервалы с наблюдениями (нечувствительного к вечности) наблюдателя О, мы рассмотрим измерительную систему О – М – R, интегральной частью которой является физический организм О. Она, как будет сказано дальше, обладает "квази-жесткостью" в смысле, определенном ниже (и как обсуждалось в Главе 14). Здесь "квази-жесткость" не означает несовершенной жесткости в смысле деформируемости под влиянием наблюдаемых пространственно-временных сил. Это означает, что для наблюдателя Q система О – М – R не сохраняет с необходимостью своей пространственной конфигурации, если она перемещается в многообразии. Для любого измерения, которое может сделать О, эта система является совершенно жесткой, но эти измерения ограничены и локальны и не могут, следовательно, согласоваться с измерениями Q. Это расхождение выражается посредством следующего набора условий.

Пусть U₁, U₂ будут направлениями пространственных и временных измерений О, и U₃ будет направлением его мгновенного существования, т.е. его "собственной вечностью". Интервалы, которые для О являются чисто время-подобными можно выразить как ∆х², интервалы пространство-подобные как ∆х¹, и интервалы вечностно-подобные как ∆х³. Измерительная система О – М – R является набором миниатюрной вселенной в истинной вселенной О. Эти направления не могут, следовательно, слишком отличаться от универсальных направлений ¹Q, ²Q, ³Q.

Следовательно, мы имеем:

1.

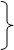U_{1 @} ¹Q

U_{2 @} ²Q (2)

U_{3 @} ³Q

где символ @ означает совпадение с точностью до бесконечно-малых первого порядка.

2. Пространство-время О ограничено до единственного уровня в вечности. Это выражается требованием, чтобы U₁ было ортогонально проекции U₂ в ³q = 0.

3. Поскольку О несовершен, а Q совершен, не может быть тождественности между направлением, заданным ортогональю 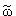к U₁U₂ и универсальным направлением вечности ³Q. С другой стороны, не может быть расхождения, ведущего к различным ситуациям на разных уровнях в вечности. Это возможно, только если 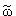составляет нуль угол с ³Q.

4. Необходимо допустить внутреннюю совместимость системы О – М – R, которая должна быть отлична от совместности Q. Этот эффект может возникнуть только внутри системы самого О. Соответственно U₃ и ³Q, вообще говоря, не будут совпадать. Однако и здесь также не может быть постоянного расхождения. Следовательно, мы должны иметь еще одно условие, заключающееся в том, что U₃ составляет нуль-угол с ³Q.

Выражение "нуль-угол" характеризует отношение между двумя векторами, имеющими одинаковые или различные составляющие, но такие, что косинус угла между ними, определенный обычным образом, равен единице. Таким образом, если единичный вектор (if, f, 1) определяет направление 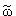в многообразии Q, то 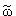составляет нуль-угол с ³Q. Тогда 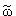косо параллельна ³Q. Четыре условия квазижесткости ведут к простому выражению для единичных векторов, определяющих направления U_j и 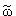(j = 1,2,3), а именно:

U₁ = (a, ib, -if)

U₂ = (ib, d, -f) (3)

U₃ = (ie, e, 1)

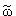= (if, f, 1)

где

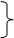a² = 1 + b² + f²

d² = 1+ b² - f² (4)

величины b, e, f все действительны и малы.

Эффект присутствия материальных объектов (вообще говоря, массивных заряженных тел) заключается в разрушении изотропии и однородности многообразия Q. Это выражается в изменении b, e, и f вместе с ^kq, где k = 1,2,3.

Можно показать, что условия интегрируемости, когда b, e, и f можно рассматривать как функции от х¹, х², вместе с характеристикой измерительной (квазижесткой) системы О приводят к закону обратной пропорциональности квадрату силы. Для целей настоящей работы можно предположить, что b, e, и f изменяются вместе с х¹, х² - т.е. они могут быть определены для каждого данного момента пространства и времени посредством измерений, которые локально выполняет О.

Date: 2015-05-18; view: 463; Нарушение авторских прав