Задача № 28

Квантовый гармонический осциллятор находится в основном состоянии. Найдите вероятность 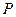обнаружения частицы в области 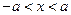, где 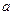- амплитуда классических колебаний.

Решение:

Квантовый гармонический осциллятор представляет собой частицу, находящуюся в потенциальном поле вида:

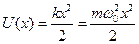(1)

График потенциальной энергии изображён на рисунке 1:

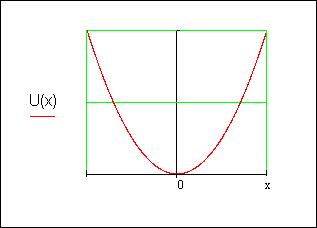
Рисунок 1

В этом случае составляют уравнение Шредингера:

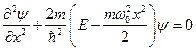(2)

Это дифференциальное уравнение имеет решение только при дискретных значениях 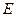. Таким образом, энергия квантового гармонического осциллятора квантуется и может принимать следующие значения:

(3)

В основном состоянии квантовое число , поэтому энергия квантового гармонического осциллятора в основном состоянии равна:

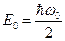(4)

Определим амплитуду классических колебаний:

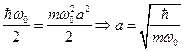(5)

Решения дифференциального уравнения (4) имеют вид:

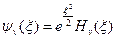(6)

где 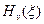- полиномы Чебышева-Эрмита, которые определяются следующим образом:

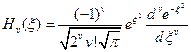(7)

где 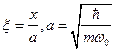. Для основного состояния , имеем пси-функцию:

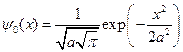(8)

Квадрат модуля пси-функции определяет плотность вероятности нахождения частицы:

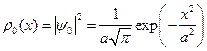(9)

Чтобы найти вероятность нахождения частицы в области 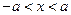нужно проинтегрировать (9) по пределам области:

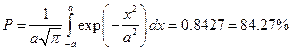(10)

Ответ:

.

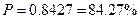Date: 2015-05-18; view: 422; Нарушение авторских прав