Электронная теория дисперсии света

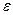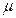Электромагнитная теория света рассматривает среды с постоянными и или 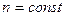, т.е. в рамках этой теории не рассматривается дисперсия света.

Для объяснения дисперсии света 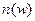Г.Лоренц разработал теорию, в основе которой лежит взаимодействие поля световой волны с электронами среды. Среда рассматривается в виде модели разряжённого газа, который состоит из отдельных диполей.

Световая волна воздействует электрическим полем 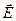на диполь, что приводит к колебанию диполя и возникновению поляризации среды.

Пусть через среду распространяется монохроматическая световая волна:

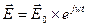(3.10)

Наличие электрического поля (3.10) приводит к поляризации среды 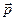, которая влияет на электрическую индукцию среды:

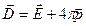(3.11)

Между векторами 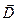индукции и 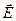напряженности существует связь:

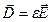(3.12)

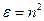
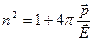
Определим дипольный момент 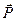, который возникает в результате воздействия электрического поля световой волны (3.10) на электроны.

Если электрон находится в электрическом поле с напряженностью 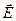, то на него действует сила Кулона F₁=eE_k (3.14)

Под действием этой силы электрон смещается от равновесного положения на величину 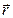, что вызывает возникновение дипольного момента

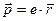(3.15)

Если среда содержит N диполей в еденице объема, то её дипольный момент равен:

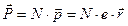(3.16)

Тогда (3.13) будет иметь вид:

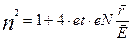(3.17)

Определим вектор смещения 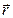, если на электрон следующие силы:

1.Сила Кулона (3.14)

2.Квазиупругая сила, которая возвращает электрон в равновесное положение

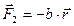(3.18)

где b- коэффициент квазиупругости.

Если на электрон действует только сила (3.18), то он совершает гармонические колебания с собственной частотой

,

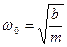где m- масса электрона.

3.Для учета потерь на излучение, которое возникает в результате колебаний электрона, Лоренц предложил учитывать эти потери за счет силы

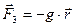(3.19)

Тогда уравнение движения электрона имеет вид:

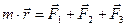(3.20)

Подставим (3.14), (3.18), (3.19) в (3.20):

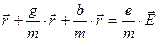(3.21)

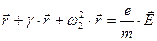(3.22)

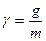- коэффициент затухания

Так как электрическое поле 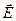изменяется по гармоническому закону (3.10) с частотой w, то решения дифференциального уравнения (3.22) будем искать в виде:

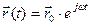(3.23)

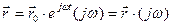
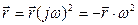
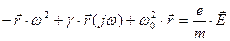
Для (3.17)

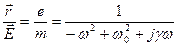(3.24)

Подставим (3.24) в (3.17)

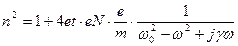(3.25)

(3.25) называется формулой Лоренца, которая показывает зависимость показателя преломления n от частоты w, то есть описывает уравнение дисперсии.

Формула (3.25) справедлива для среды, которая имеет диполи с одной собственной частотой w₀ (частота поглощения). Если сфера имеет диполи с частотами w_oi, то можно показать, что (3.25) в этом случае имеет вид:

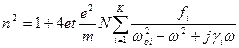(3.26)

Где f_i- доля i-тых диполей в концентрации N (сила осцелятора)

К- количество типов диполей.

Формула Лоренца (3.25) справедлива для модели идеального газа.

Если атомы находятся на малом расстоянии друг от друга, то их дипольные моменты влияют друг на друга, что вызывает изменения напряженности электрического поля, которое воздействует на диполь. Эти изменения поля учитываются полем Лоренца.

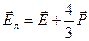(3.27)

В этом случае формула (3.25) записывается в виде:

(3.28)

(3.28) называется формулой Г. Лоренца – Л. Лоренца. Она справедлива, если g=0 (вдали от линии поглощения).

Date: 2015-05-18; view: 671; Нарушение авторских прав