Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Распределение числа частиц по высоте.Распределение Больцмана.Распределение Максвелл-Больцмана
|
|
При выводе основного уравнения молекулярно-кинетической теории газов и максвелловского распределения молекул по скоростям предполагалось, что на молекулы газа внешние силы не действуют, поэтому молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул-с другой, приводят к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает.Выведем закон изменения давления с высотой.Разность давлений р и p+ d p равна весу газа, заключенного в объеме цилиндра высотой d h с основанием площадью 1 м2: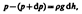 
где r — плотность газа на высоте h (d h настолько мало, что при изменении высоты в этом пределе плотность газа можно считать постоянной). Следовательно, 
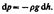(1), pV=(m/M)RT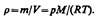 
Подставив это выражение в (1), получим 
С изменением высоты от h 1 до h 2 давление изменяется от р 1 до р 2 т. е. 
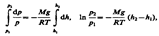или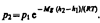 
(2)Выражение (2) называется барометрической формулой. 
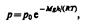(3)где р — давление на высоте h, p=nkT: 
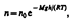где n- концентрация молекул на высоте h, n 0-то же, на высоте h= 0. 
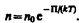- распределение Больцмана для внешнего потенциального поля.Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.
При рассмотрении распределения Максвелла — Больцмана, бросается в глаза важное свойство — его можно представить как произведение двух множетелей: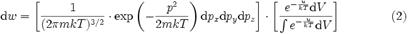 
.
Первый множитель есть ничто иное как распределение Максвелла, оно характеризует распределение вероятностей по импульсам. Второй множитель зависит только лишь от координат частиц и определяется видом её потенциальной энергии. Он характеризует вероятность обнаружения частицы в объеме dV.Согласно теории вероятности, распределение Максвелла — Больцмана можно рассматривать как произведение вероятностей двух независимых событий — вероятность данного значения импульса и данного положения молекулы. Первая из них: 
представляет распределение Максвелла;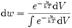 
-распределение Больцмана.
Date: 2015-05-09; view: 2517; Нарушение авторских прав