Квантовые статистики. Распределение Ферми-Дирака и Бозе-Эйнштейна

Квантовая статистика исследует физические свойства систем одинаковых микрочастиц(электронов, фотонов и т.д.) Поведение совокупности частиц одного сорта описывается волновой функцией.Квантовая статистика допускает 2 класса функций: симметричные, сохраняющие свой знак при перестановке двух частиц: антисимметричные, меняющие знак при перестановке.Одним из важнейших «объектов» изучения квантовой статистики, как и классической, является идеальный газ.Состояние сис-мы невзаимодействующих частиц задается с помощью так называемых чисел заполнения Ni — чисел, указывающих степень заполнения квантового состояния (характеризуется данным набором i квантовых чисел) частицами сис-мы. Для систем частиц, образованных бозонами частицами с нулевым или целым спином, числа заполнения могут принимать любые целые значения: 0, 1, 2,... Для систем частиц, образованных фермионами - частицами с полуцелым спином, числа заполнения могут принимать лишь два значения: 0 для свободных состояний и 1 для занятых. Идеальный газ из бозонов — бозе - газ — описывается квантовой статистикой Бозе-Эйнштейна.Распределение бозонов по энергиям вытекает из так называемого большого канонического распределения Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым: (1)Это распределением Бозе-Эйнштейна. Здесь <Ni>-среднее число бозонов в квантовом состоянии с энергией Еi, k-постоянная Больцмана, Т—термод-я темп-ра, µ - химический потенциал. Химический потенциал находится обычно из условия, что сумма всех <Ni> равна полному числу частиц в системе. Здесь µ<=0, так как иначе среднее число частиц в данном квантовом состоянии отрицательно, что не имеет физического смысла. Он определяет измен-е внутренней энергии сис-мы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внут-я энергия (энтропия, объем), фиксированы.Идеальный газ из фермионов — ферми-газ — описывается квантовой статистикой Ферми-Дирака. Распределение фермионов по энергиям имеет вид (2) где <Ni> — среднее число фермионов в квантовом состоянии с энергией Еi, µ — химический потенциал. В отличие от (1) µ может иметь положительное значение (это не приводит к отрицательным значениям чисел <Ni>. Это распределение называется распределением Ферми — Дирака.

2.8Квантовая теория теплоёмкости Эйнштейна

Квантовая теория теплоёмкостей Эйнштейна была создана Эйнштейном в 1907 году, при попытке объяснить экспериментально наблюдаемую зависимость теплоёмкости от темп-ры.При разработке теории Эйнштейн опирался на следующие предположения:1Атомы в кристаллической решетке ведут себя как гармонические осцилляторы, не взаимодействующие друг с другом.2Частота колебаний всех осцилляторов одинакова.3Число осцилляторов в 1 моле вещества=3Na.4Энергия их квантована 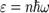, ,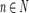5Число осцилляторов с различной энергией определяется распределением Больцмана: 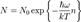Внут-я энергия 1 моля вещества: 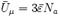, 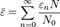и составляет: 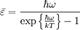,отсюда: 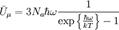Определяя теплоёмкость как производную внутренней энергии по температуре, получаем окончательную формулу для теплоёмкости: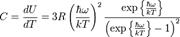

Date: 2015-05-09; view: 1146; Нарушение авторских прав