Второе начало термодинамики. Условие эволюции для изолированной системы

Второе начало термодинамики имеет несколько эквивалентных формулировок и две части. Мы используем первую часть так. В дифференциальной форме первого начала термодинамики

d q = d u + p d v + ∑ A_j d a_j - ∑m _k d N_k, (1)

изменение d q в квазиравновесной системе всегда можно представить через полный дифференциал однозначной функции термодинамического состояния, называемой энтропией, согласно формуле (формулировка Клаузиуса)

d q = T d s,

т.е. 1/ T является интегрирующим множителем для (1). В общем случае при наличии необратимых процессов внутри системы d s = d s_ext + d s_in. Индексы _ext и _in в соответствии с физическим смыслом обозначают внешний и внутренний. Здесь d s_ext – изменение энтропии системы, обусловленное обменом энергией и веществом с ОС, а d s_in – изменение энтропии, обусловленное необратимостью процессов внутри системы. Для закрытой системы, которая не обменивается веществом с внешней средой, d s_ext = d q / T. Величина d s_ext может быть положительной и отрицательной, а d s_in – только большей или равной нулю. В изолированной системе d s_ext = 0.

Вторая часть II начала термодинамики утверждает, что в изолированной системе (d s_ext = 0) могут происходить только процессы, сопровождаемые ростом энтропии, т.е. s = d s_in /d t = d s /d t > 0 (d t > 0). Функцию s называют производством энтропии. Отсюда следует, что для всякого неквазистатического процесса, протекающего в ТС T d S > d Q где d Q - количество тепла, поглощенного системой при неравновесном (неквазистатическом) переходе из 1-го состояния во 2-е, такое, что d S = S ₂ - S ₁. Отметим, что все другие экстенсивные параметры (кроме энтропии) в изолированной системе сохраняются (остаются неизменными).

Рис. 5. отстствует блин

В состоянии равновесия энтропия изолированной системы достигает максимума. При этом термодинамическое равновесие соответствует наибольшей степени неупорядоченности системы. Данное обстоятельство обосновывается в статистической физике при определении энтропии в терминах теории вероятности. В то же время неотрицательная функция s, имеющая нуль в равновесной точке должна иметь в этой точке минимум. Поэтому имеем d s £ 0. Данное неравенство называют условием эволюции. Знак равенства относится к равновесному состоянию. Таким образом, изолированная система эволюционирует до тех пор, пока производство энтропии не станет равным нулю.

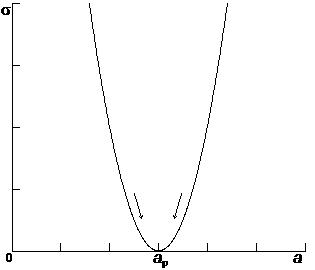
Рис. 6.

Экстремальные свойства функций S и s при отмеченных условиях приводят к определенным неравенствам для физических величин, обычно называемых условиями устойчивости. В частности, опираясь на это, выводятся неравенства C_v > 0 и (¶p/¶ v) _T < 0.

Более того, идет ли речь об изолированных, закрытых или открытых системах, всегда выполняется неравенство d S_in ³ 0. Это и есть самая общая формулировка второго начала термодинамики. Важно, что она применима не только ко всей системе, но и ко всем подсистемам. Например, если разделить систему на две части (подсистемы) то выполняется не только неравенство

d S_in = d S_in¹ + d S_in² ³ 0

где d S_in¹, d S_in² - энтропии, произведенные в каждой подсистеме, но и неравенства

d S_in¹ ³ 0, d S_in² ³ 0.

Однако никогда не может быть такого, чтобы

d S_in¹ ³ 0, d S_in² < 0 и d S_in = d S_in¹ + d S_in² ³ 0.

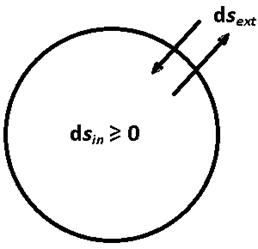
Рис. 7.

Аналогичные формулировки 2-го начала термодинамики возможны и для не изолированных систем. Если, например, в системе с постоянным числом частиц (N = const) поддерживается постоянная температура (изотермический случай T = const) и не совершается работа d l = 0 (d v = 0), то вместо D S ³ 0, будет выполняться неравенство D F £ 0, где F = U - TS — свободная энергия. Знак (=) относится к обратимым процессам, (<) - к необратимым.

18. Причины необратимости реальных термодинамических процессов. Влияние трения на процесс истечения.

Date: 2015-05-09; view: 679; Нарушение авторских прав