Термодинамические параметры состояния и их функции

При делении системы пребывающей в равновесии на части равновесие не нарушается. Имеется только два класса термодинамических величин.

1. Если значение термодинамической величины при делении системы на части ведет себя так:

F _общ = F ₁ + F ₂,

то такую величину называют экстенсивной. Примеры: число частиц N, объем тела V. Экстенсивная величина пропорциональна числу частиц в системе.

2. Если значение термодинамической величины при делении системы сохраняется для каждой ее части

f _общ = f ₁ = f ₂,

то такую величину называют интенсивной. Интенсивная величина не зависит от числа частиц в системе. Таким образом равновесное состояние однородной системы является внутренним свойством, определяемым интенсивными параметрами. Примеры: температура T, давление p, химический потенциал m.

Основные параметры: T – ^° K (t – ^° C), p – Па, удельный объем v = 1/r, r –кг/м³, удельные внутренняя энергия u – Дж/кг, энтальпия h – Дж/(кг´град), энтропия s – Дж/(кг´град). Имеют место формулы

h = u + pv,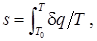

где температура T ₀ соответствует началу отсчета энтропии, T – температура рабочего тела, d q – приращение тепловой формы энергии в процессе. Последнее равенство – одна из формулировок второго начала термодинамики, определяющего энтропию как функцию состояния системы для обратимых процессов, определение которых будет дано позже.

Отметим, что переход к удельным величинам для экстенсивных параметров превращает их в интенсивные. Это удобно при составлении таблиц свойств и диаграмм для состояния систем, но в некоторых случаях различие интенсивных и экстенсивных переменных существенно.

Для систем типа газа состояние термодинамического равновесия может быть полностью охарактеризовано заданием двух параметров (напр. p и T). Любой третий параметр будет определенной функцией их. В частности, уравнение состояния идеального газа (Менделеева-Клапейрона) имеет вид

pv = RT,

где R = R _m/m, R _m = 8314 Дж/(кмоль´град) – удельная газовая постоянная, m – молекулярный вес. Данное уравнение называют термическим уравнением состояния идеального газа. Оно представляет собой поверхность (термодинамическую) в трехмерном пространстве p, v, T. В термодинамике вводится еще калорическое уравнение состояния. Термодинамическая система считается заданной, если наряду с ним известно еще термическое(ие) уравнение состояния. Для идеального газа калорическое уравнение формулируется как независимость внутренней энергии газа от его объема. В рамках термодинамики уравнения состояния (которых может быть несколько) считаются заданными (либо эмпирически, либо определяются методами статистической физики) при формулировке ТС.

4. Сухой насыщенный пар. Линия насыщения. Влажный пар, определение параметров влажного пара, степень сухости влажного пара. Перегретый пар.

Date: 2015-05-09; view: 505; Нарушение авторских прав