Причины необратимости реальных термодинамических процессов

Выделим следующие основные причины необратимости реальных процессов:

1. Наличие в рабочем теле градиентов основных параметров, которые приводят к диссипации механической энергии, т.е. необратимому переходу ее в тепловую энергию.

2. Наличие внешнего трения.

3. Возрастание энтропии, которая является мерой необратимости при передаче тепла от рабочего тела с большей температурой к рабочему телу с меньшей температурой (D Q _х = - D Q _г = D Q):

D s _г = -D Q / T _г < 0, D s _х = D Q / T _х > 0, (D Q > 0).

Мы опустили индекс _in при s, т.к. D s_ext = 0. Общий прирост энтропии при отсутствии других переходов энергии (T _г > T _х)

D s = D s _г + D s _х = D Q (1/ T _х - 1/ T _г) > 0.

Отметим, что вся система изолирована, поэтому D s > 0. Однако для ее части (горячей) D s _г < 0.

4. При образовании ударных волн в аппаратуре, даже в условиях адиабатичности.

Пример отличия обратимого (теоретического) и реального необратимого течений газа через сопло.

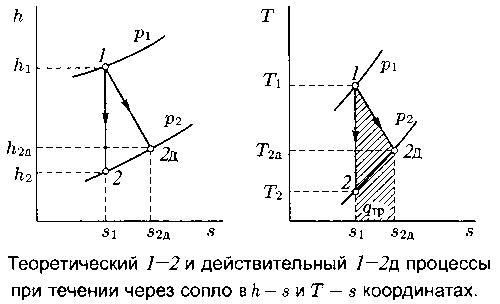
Рис. 8.

Теоретические и действительные процессы при течении через сопло. В сопле d q _тр > 0, d q _внеш = 0, p ₁ > p ₂.

Имеем следующее выражение для действительной скорости W _2д:

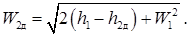W ₁ << W ₂; h _2д > h ₂ Þ W _2д < W ₂; W _2д = j W ₂,

j Î (0.95, 0.98) - скоростной коэффициент для шлифованных сопел.

19. Дросселирование: уравнение процесса. Изменение параметров рабочего тела при дросселировании, эффект Джоуля-Томсона.

Изменение параметров рабочего тела при дросселировании. Дроссель эффект. Явление инверсии.

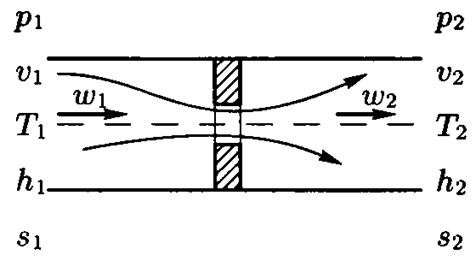
Рис.1

В нашем курсе мы рассматриваем дросселирование только как адиабатический (d q = 0) неравновесный процесс без совершения работы (d l = 0) при прохождении через сужение в канале, сопровождаемый понижением давления. При необратимом дросселировании наблюдается возрастание энтропии (s ₂ > s ₁). Имеем также p ₂ < p ₁, v ₂ > v ₁, и из ранее установленного уравнения при d q = 0 (адиабатический процесс) находим:

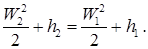
Скорость потока среды в технических трубопроводах невелика, поэтому обычно полагают W ₂ = W ₁ = 0. Кроме того, часто значение скоростей на входе и выходе отличается незначительно, т.е. W ₂ @ W ₁, что позволяет не учитывать вклад этих скоростей и в более общих случаях. В таком случае имеем

h ₂ = h ₁,

или

u ₂ + p ₂ v ₂ = u ₁ + p ₁ v ₁.

Уравнение процесса адиабатического дросселирования h ₁ = h ₂ следует трактовать так: оно относится к сечениям, удаленным от дросселя, и лишь указывает на постоянство энтальпии потока до и после дросселирования в этих, относительно удаленных сечениях. В ходе же самого необратимого процесса дросселирования характер изменения энтальпии более сложный (если ее можно ввести локально) и не описывается данным уравнением. Поэтому следует на термодинамических диаграммах процесс дросселирования изображать пунктиром, как и любой необратимый процесс, где лишь определенно известны начальное и конечное состояния.

Если p ₂ v ₂ = p ₁ v ₁, то u ₂ = u ₁ Þ T ₂ = T ₁ для идеального газа, когда u = u (T) – монотонно возрастающая функция, т. е. для идеального газа эффект изменения температуры (Джоуля-Томсона) отсутствует. (Зависимости p ₂ v ₂ = p ₁ v ₁ и T ₂ = T ₁ также согласуются с уравнением Менделеева-Клапейрона.) Для характеристики эффекта Джоуля-Томсона вводится коэффициент адиабатического дросселирования, или дифференциальный дроссель эффект

a = d T /d p. (1)

Для него при наших предположениях имеет место формула

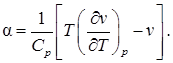(2)

Интегральный дроссель эффект можно рассчитать по зависимости

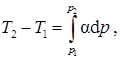
вытекающей из (1). Если D T > 0, то говорят, что эффект положительный, иначе при D T < 0 – отрицательный. Температура при которой a = 0 называется температурой инверсии. При температуре инверсии эффект Джоуля-Томсона меняет знак. Например, для газа Ван-дер-Вальса

(p + a / v ²)(v – b) = RT, (a, b – const)

расчет параметра a по соотношению (2) дает приближенное выражение

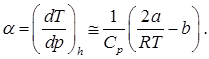
При этом a и b считаем малыми, пренебрегая слагаемыми второго порядка a ² и b ², а газ – достаточно разреженным: v = 1/r >> b. Отсюда видно, что

T_inv = 2 a /(Rb).

Для большинства газов (кроме водорода и инертных газов) при обычных (комнатных) температурах a > 0. Температура инверсии для всех газов лежит значительно выше критической. Например, при атмосферном давлении t_inv = –57° C – для кислорода, t_inv = –239° C – для гелия – самая низкая температура инверсии.

20. Явление инверсии, интегральный и дифференциальный дроссель-эффекты.

Учебник страница 39. осторожно, там опечатка. Вместо p2v2>p1v1 читай p2v2<p1v1 после слов «И наоборот, если».

21. Элементы неравновесной термодинамики. Движущие силы процессов при отклонении от равновесия.

Элементы неравновесной термодинамики. Движущие силы процессов при отклонении от равновесия.

Для определенности считаем систему в целом изолированной и в ней будем рассматривать состояния близкие к равновесным. Т. е. будем говорить о слабонеравновесных изолированных системах. Пусть x _k – совокупность макроскопических (экстенсивных) параметров, характеризующих отклонение от равновесного состояния, для которого все x _k = 0. Например, если в равновесном состоянии число частиц в системе равно N_p, то в качестве x₁ можно взять отклонение D N = N – N_p от состояния равновесия x₁ = D N. При равновесии, согласно 2-му началу термодинамики, энтропия имеет максимум, т. е. ¶ S /¶x _k = 0 при всех k. Кроме того состояние равновесия системы устойчиво ко всем флуктуациям параметров вблизи точки равновесия, приводящим к уменьшению энтропии D S < 0. Далее в системе происходят необратимые процессы, сопровождаемые ростом энтропии и в результате снова достигается равновесие: S = S _max. В частности, при флуктуации температуры условие устойчивости приводит к необходимости выполнения неравенства C_v > 0.

В случае функции одного переменного о поведении данной функции в окрестности некоторой точки хорошее представление дает ее аппроксимация линейной функцией – дифференциалом. Однако в точке экстремума производная обращается в нуль и нетривиальные свойства функции определяются первым ненулевым слагаемым ее разложения в ряд Тейлора в окрестности экстремума. Для слабонеравновесной теории будет достаточно сохранения квадратичного слагаемого

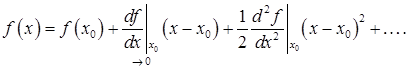
В термодинамике подобный вариант для одной независимой переменной имеет право на существование, однако значительно интереснее и важнее случай нескольких переменных. Фактически теорию полностью иллюстрирует случай 2-х переменных. Большее число переменных приводит только к некоторому усложнению записи и анализа конкретных ситуаций. Поэтому ограничимся случаем k = 2 и обозначим независимые переменные x и h (x₁ = x, x₂ = h).

Разложим энтропию в ряд Тейлора в окрестности равновесного состояния

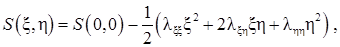
где параметры l _ij определены при равновесных условиях:

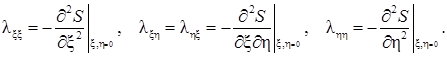
Слагаемые третьего порядка ряда Тейлора отброшены, а знаки минус введены с целью сделать параметры l_xx и l_hh положительными. Определим соответствующие переменным x и h «обобщенные силы» (они так называются, поскольку вызывают релаксацию к равновесию)

D S = S (x,h) – S (0,0). (1)

Отметим, что силы X _x и X _h при наших ограничениях связаны с координатами x и h линейно. Введем соответствующие координатам x и h потоки (экстенсивных переменных)

J _x = dx/d t, J _h = dh/d t.

Величины этих потоков определяются не только свойствами данной системы, но и отклонениями величин x и h от равновесия, т.е. J _x,h(x,h), причем J _x,h(0,0) = 0 – в состоянии равновесия. В отличие от равновесной термодинамики в теории появляется время. Масштаб этого времени значительно превышает характерное время молекулярного взаимодействия.

22. Связь потоков и сил. Соотношения Онзагера.

Связь потоков и сил. Соотношения Онзагера.

При малых x и h можно ограничиться в формулах для потоков J _x,h(x,h) линейными по x и h слагаемыми, или, в силу (1), линейными по X _x и X _h, т. е.

J _x = L _xx X _x + L _xh X _h = l _xxx + l _xhh, (2)

где

l _xx = L _xxl_xx + L _xhl_hx, l _xh = L _xxl_xh + L _xhl_hh, l _hh = L _hhl_hh + L _hxl_xh.

Для функций J _h достаточно в выписанных формулах заменить x «h.

Онзагер обосновал симметричность матрицы коэффициентов L _xh = L _hx, которая имеет место при любом числе параметров x _k. Физический смысл условия L _xh = L _hx состоит в том, что поток J _x, вызываемый силой X _h такой же как поток J _h вызываемый силой X _x. Теория Онзагера описывает линейную релаксацию значений экстенсивных переменных к их равновесным значениям.

Выражение (2) ограничивает теорию рассмотрением только линейных эффектов в неравновесной термодинамике. Отметим, что именно линейные эффекты являются основными в задачах диффузии, теплопроводности, вязкого трения и т. п., в которых в качестве исходных положений используются известные из экспериментов соотношения, выражающие прямую пропорциональность величин стационарных потоков градиентам соответствующих параметров. В частности закон Фурье (1822 г.) для теплопроводности, Фика (1855 г.) для диффузии, Ома (1826 г.) для электрической проводимости.

Одна из задач теории и практики рассматриваемых слабонеравновесных необратимых процессов состоит в установлении универсальных связей между кинетическими коэффициентами, характеризующими разные процессы переноса в данной системе. Число независимых соотношений в матрице L в силу соотношений взаимности Онзагера

L_ij = L_ji, i, j = 1, 2, …, n;

Рис. 1

равно 1 + 2 + 3 + … + n = n (n + 1)/2 согласно формуле арифметической прогрессии.

23. Скорость возрастания энтропии. Внешнее и внутреннее изменение энтропии открытой системы.

Скорость возрастания энтропии.

Имеем (зависимость от времени для энтропии только через функции x и h)

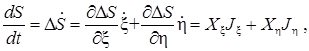(1)

согласно определению потоков и сил. Важно отметить, что отдельные слагаемые в сумме (1) (и ее обобщении на число параметров большее двух) могут быть отрицательными. Положительной, в силу второго начала термодинамики, должна быть вся сумма. Таким образом становятся возможными процессы при убывании энтропии, если они сопровождаются дополнительными процессами с приростом энтропии, большим по абсолютной величине. {Пример частичного разделения веществ невозможный без перекрестного эффекта - термодиффузия}.

Имеют место формулы

d S /d t = L _xx X _x² + 2 L _xh X _x X _h + L _hh X _h² = F_xxx² + 2F_xhxh + F_hhh², (2)

где

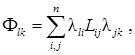
и использованы ранее установленные связи потоков и сил. Последняя формула выписана для общего случая. При n = 2 можно считать индекс 1 равным x, а 2 – h. Согласно II части второго начала термодинамики s = d S /d t (производство энтропии) должно быть неотрицательной величиной

d S /d t ³ 0.

Данное условие – требование положительной определенности квадратичных форм (2), в частности

s = d S /d t = L _xx X _x² + 2 L _xh X _x X _h + L _hh X _h², (3)

налагает определенные требования на коэффициенты переноса, а именно

L _xx > 0, L _hh > 0, L ²_xh < L _xx L _hh. (4)

Первые два неравенства (4) получаются как частные случаи (3) при X _x = 0 и X _h = 0 соответственно. Если выделить при X _h ¹ 0 в (3) положительный множитель X _h², то для переменной z = X _x/ X _h получим квадратный трехчлен L _xx z ² + 2 L _xh z + L _hh (второй множитель). Как известно, при L _xx > 0 это выражение будет положительно при любых z если дискриминант L ²_xh – L _xx L _hh будет отрицательным, что и выражает третье неравенство (4). В простейших случаях неравенства (4) приводят к положительности коэффициентов теплопроводности и диффузии

k > 0 и D > 0.

Наше рассмотрение относилось к случаю изолированной, слабонеравновесной системы. Изложенная выше теория применима также для открытых систем при незначительном отклонении от равновесия. Если система не изолирована (открыта), то

d S = d S_e + d S_i; e – external, i – internal,

где d S_e = d Q / T – изменение энтропии за счет квазистатического процесса, связанного с обменом энергией с окружающими системами, d S_i – изменение энтропии за счет происходящих в самой системе неравновесных (диссипативных) процессов, таких как теплопроводность, диффузия, вязкое трение и т. п.

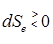, d S_i = , (d t > 0, 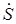> 0), d S_i > 0.

При d S_i << |d S_e | мы возвращаемся к квазистатической термодинамике.

Отметим два существенных, основных положений линейной термодинамики. 1. Возможность существования открытой системы в стационарном неравновесном состоянии, в котором внутреннее производство энтропии компенсируется ее оттоком из открытой системы. 2. Сопряжение динамических процессов, благодаря которому в открытой системе процесс, невозможный в отсутствии сопряжения (перекрестных эффектов), так как сам по себе он связан с понижением энтропии, реализуется за счет свободной энергии других, энтропийно выгодных процессов.

24. Перенос тепла между двумя телами за счет теплопроводности. Примеры перекрестных эффектов переноса.

Перенос тепла между двумя телами за счет теплопроводности.

Рис.2. Нету. И в учебнике не нашла.

Считаем, что перегородка между телами, через которую осуществляется процесс переноса, замедляет релаксационный процесс настолько, что в каждый момент времени в подсистемах 1 и 2 реализуется равновесное термодинамическое состояние. Первый закон термодинамики

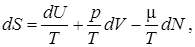(1)

используем для системы рис. 2 при d v = 0 и d N = 0. В таком случае d Q = d U, поэтому говорим о теплопроводности (переноса тепла). Два изменяющихся экстенсивных параметра в данном случае U ₁ и U ₂. Общее для 1-го и 2-го резервуаров значение равновесной температуры обозначим T _p. Из формулы (1) и определения обобщенных сил, видим, что переменным U ₁ и U ₂ соответствуют термодинамически сопряженные интенсивные величины 1/ T ₁ и 1/ T ₂. Термодинамически сопряженными называют пару термодинамических параметров, образующих выражение вида A d a в соотношениях типа (1). Из принципов Онзагера следует, что

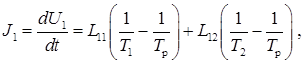(2)

(3)

В данном случае dU_j / dt – потоки J_j, а термодинамически сопряженные (см. (1)) величины (интенсивные переменные) образуют, как можно показать, силы (X _1,2 = (1/ T _1,2 – 1/ T _p). Обратим внимание, что движущей силой теплопроводности является D(1/ T) а не обычно (эмпирически) используемая разность температур D T. Это фундаментальный вывод теории Онзагера, имеющий отношение и к другим движущим силам процессов переноса.

Здесь L симметричная и положительно определенная матрица L_ij = L_ji. Два резервуара образуют изолированную систему. Поэтому, по закону сохранения энергии любая потеря энергии телом 1 должна в точности компенсироваться увеличением энергии тела 2, т.е. U ₁ + U ₂ = const и d(U ₁ + U ₂)/d t = 0. Следовательно, сумма правых частей уравнений (2) и (3) должна быть всегда равна нулю при любых T ₁ и T ₂. Так может быть только в том случае, если L ₁₁ = – L ₂₁ и L ₂₂ = – L ₁₂. Учитывая, что L ₁₂ = L ₂₁ – (соотношение симметрии), получаем L ₁₁ = – L ₂₁ = – L ₁₂ = L ₂₂ = L, где L – некоторая неотрицательная величина (это следует из условия 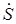> 0 или из теорем линейной алгебры, см. (4) выше).

Теперь уравнение (2) можно переписать так

(4)

где последнее равенство – приближенное. Оно выполняется при малых значениях | T ₂ – T ₁|. Уравнение (4) означает, что тепло в среднем переходит от более нагретого тела к менее нагретому, причем скорость переноса тепловой энергии пропорциональна разности обратных температур, или приближенно – разности (следите за индексами) температур. Последнее утверждение известно как закон остывания Ньютона, на термодинамическом уровне описания представляет собой аналог закона теплопроводности Фурье.

Теория Онзагера нашла хорошее экспериментальное подтверждение при описании перекрестных эффектов (в нашем случае их представляет коэффициент L _xh при x ≠ h). Например, при наличии градиентов химического потенциала и температуры диффузионный поток определяется этими градиентами, а не только градиентом химического потенциала. Зависимость диффузионного потока от градиента температуры называют термодиффузией. Кроме того, градиент химического потенциала вызывает поток теплоты (диффузионный перенос тепла, причем L_NT = L_TN). Эмпирически это было получено в виде

J_N = – D D n – D_T DJ, J_T = – k _N D n – kDJ, J = kT,

где k – постоянная Больцмана. Теория Онзагера позволяет установить связь между коэффициентом диффузии D, термодиффузии D_T и коэффициентом диффузионного переноса тепла k _N. Для идеального газа эта зависимость выглядит так

k _N = J² D_T / n + 3J D /2.

Встречаются также эффекты бародиффузии, явление Пельтье (выделение тепла при прохождении электрического тока через спай) и др. Работа термопары при определении температуры среды в определенной точке также основана на перекрестном эффекте (термоЭДС) – возникновение разности потенциалов на концах разомкнутой электрической цепи, состоящей из последовательно соединенных проводников, изготовленных из разных материалов, в случае, когда спаи поддерживаются при разных температурах.

Теория Онзагера оперирует с небольшими (линейными) отклонениями от состояния равновесия. При более глубоком (нелинейном) отклонении от равновесия возникает ряд специфических эффектов, связанных с образованием определенных диссипативных структур. Эти структуры, в частности, представляют огромный интерес для биологии. Их исследование находится на переднем крае биологической науки.

Date: 2015-05-09; view: 3601; Нарушение авторских прав