Интегральные соотношения энергии и диффузии

В качестве исходных используются дифференциальные уравнения энергии в формуле Широкова (7.42)

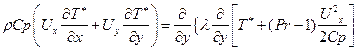
и умноженное на энтальпию торможения СрТ^*_∞ уравнение неразрывности (7.5) или, для несжимаемой среды (7.11).

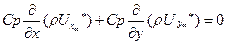(7.66)

Вычитая (7.66) из (7.42) и интегрируем по у от 0 до ∞(практически до у = δ_т получаем 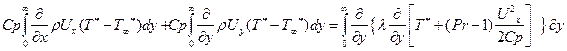(7.67)

Используются граничные условия при у = 0, U_x = U_xcт, U_у = U_уcт, Т^* = Т_ст^*; при у =δ_т^**, U_x = U_∞, U_у = 0, Т^* = Т_∞^*;

Второй определенный интеграл в правой части (7.67) вычисляется как

, а интеграл в правой части равен

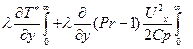
С учетом (7.56) получаем из (7.66):

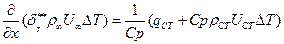(7.68)

где ΔТ = Т_ст – Т^*_∞,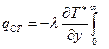

При известных ρ_∞(х), U_∞(х), ΔТ(х), q_ст(х) U_ст(х) уравнение(7.68) решается с граничным условием х = 0, δ_т^** = δ_то^**. Решение проводится численно, например, методом Рунге-Кутта. В результате решения получаем распределение δ_т^** = δ_то^**(х).

Введя число Стантона

в уравнение (7.68) получаем

(7.69)

Аналогично предшествующему выводу получается соотношение диффузии в пограничном слое. Для этого используются уравнения диффузии i – ого компонента (7.29) и уравнение неразрывности (7.11), умноженное на 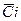. Интегральное соотношение диффузии приобретает вид

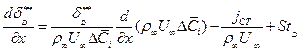(7.70)

где - диффузионное число Стантона.

Удобной формой записи уравнений (7.63), (7.68), (7.70) является следующая:

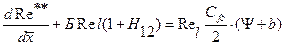(7.71)

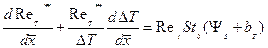(7.72)

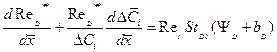(7.73)

где 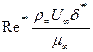, , 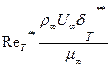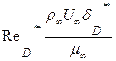- характерные числа Рейнольдса динамического, теплового и диффузионного пограничных слоев; С_f0. St_D0 – коэффициент трения и тепловое и диффузионное числа Стантона в стандартных условиях на плоской пластине при тех же числах Рейнольдса,

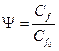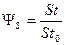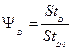, , - относительные законы трения, теплообмена и массообмена при тех же числах Рейнольдса;

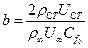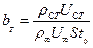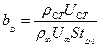, , - относительные динамический, тепловой и диффузионный параметры проницаемости стенки.

Date: 2015-05-09; view: 672; Нарушение авторских прав