Уравнение теплопроводности в неподвижной и в движущейся среде

Рассмотрим среду, за­пол­нен­ную движущейся не­сжи­ма­емой жидкостью, и выделим (мы­с­лен­но) не­под­виж­ный объ­ем V, ограниченный зам­к­ну­той по­верх­ностью S (см. ри­су­нок). Вы­де­лим на этой по­верх­ности ма­лый учас­ток dS с век­тором нор­ма­ли 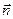. Так как участок выб­ран про­из­воль­но, то на­прав­ление век­то­­ра нормали, вообще го­воря, не сов­падает ни с на­прав­ле­ни­ем век­­тора гра­ди­ен­та тем­пе­ра­ту­ры, ни с на­прав­ле­ни­ем век­тора ско­рос­ти. Ко­личество теп­ла, про­те­ка­ю­щего за единицу вре­мени че­рез этот участок, оп­ре­деляется сум­­мой потоков теп­ла за счет теп­ло­­про­вод­нос­ти и кон­век­­ции. Тепловой поток за счет теп­ло­про­вод­ности пропорционален про­ек­ции вектора гра­ди­ен­та температуры на век­­тор нор­ма­ли: 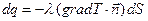, а конвективный поток найдем следую­щим об­ра­зом. Умножив скалярно вектор ско­рос­ти 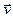на вектор нормали 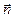к участку dS, найдем про­­ек­цию скорости на вектор нормали. Умножив эту проекцию на площадь dS, найдем объем жид­кости, протекающей за единицу времени через участок dS. Умножив этот объем на плот­ность r, найдем массу, а умножив мас­су на удельную теплоемкость c и температуру T, най­дем ко­ли­чест­во тепла, которое вместе с дви­жущейся жидкостью протекает за единицу вре­ме­ни че­рез участок dS; это и есть кон­век­тив­ный поток 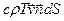. Таким об­ра­зом, суммарный тепловой по­ток че­рез участок dS равен:

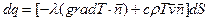, (1)

а ко­ли­­чество тепла, про­те­ка­ю­ще­го за еди­ни­цу времени через всю поверхность S, равно ин­тег­ра­лу от dq по этой по­верх­ности:

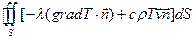. (2)

Внутри объема V могут действовать ис­точ­ни­ки те­п­ла. Например, в сре­де могут идти химические реакции с выделением или по­глощением теп­ла; может выделяться джоулево тепло, ес­ли течет электрический ток; может происходить вы­­де­ле­­ние тепла в результате поглощения электромагнитного из­лучения и т.п.; работа сил вязкости при движении жидкости также приводит к вы­де­ле­нию тепла. Обозначим через f(x,y,z,t) ко­ли­чест­во вы­деляемого или по­гло­ща­е­мо­го тепла в единицу вре­ме­ни в единице объ­е­ма, причем бу­дем считать эту функцию положительной, если тепло вы­­де­ля­ет­ся, и от­ри­ца­тель­ной, если поглощается; раз­мер­ность этой функции: Вт/м³. С учетом всего этого, ба­ланс энер­­гии вы­де­лен­но­го объема V принимает вид:

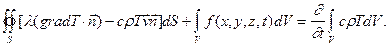(3)

Полученное равенство можно назвать уравнением теплопроводности в движущейся не­сжи­маемой жидкости в ин­тегральной фор­­ме. Первый интеграл в левой части выражает ко­ли­чест­во тепла, про­те­ка­ю­ще­го за еди­ни­цу времени че­рез поверхность S, второй - количество теп­ла, вы­де­лив­ше­е­ся или по­гло­тив­ше­еся (в зависимости от знака функции f) в объеме V за еди­ни­цу времени, а пра­вая часть выражает изменение количества тепла, находящегося внутри объ­е­ма V, за еди­ницу вре­­ме­ни. Знак пе­ред пер­вым интегралом в левой части уравнения (3) выб­ран в соответствии с физическим смыслом про­ти­во­­по­ло­жно зна­ку в формуле (2), т.к. теп­ло­вой поток считается положительным, если он втекает в объем, и от­ри­ца­тельным, если вы­те­ка­ет из объема.

Чтобы преобразовать уравнение (3) к дифференциальной форме, применим к интегралу по поверхности (к первому интегралу в левой части) теорему Остроградского-Гаусса:

.

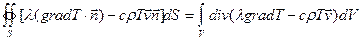Подставляя в (3), получаем:

.

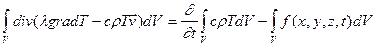Ввиду произвольности объема V находим:

,

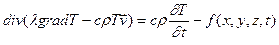или

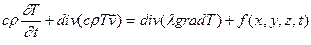. (4)

Из векторного анализа известно, что если 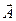- векторное поле, а U - скалярное поле, то 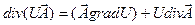. Воспользуемся этим равенством, чтобы раскрыть второе сла­га­е­мое в левой части уравнения (8.4). Считая, что cr = const, находим:

,

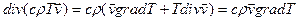т.к. для несжимаемой жидкости .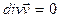

Таким образом, уравнение теплопроводности в несжимаемой жидкости можно записать в следующем общем виде:

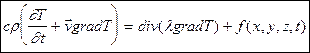. (5)

Если l = const, то div(lgradT) = ldiv(gradT) = l D T. Разделив обе части уравнения (5) на cr, получаем уравнение теплопроводности в движущейся несжимаемой жидкости в "стан­дарт­ном" виде:

. (6)

Если объемное тепловыделение отсутствует (в том числе, если можно пренебречь ра­бо­той сил вязкого трения, например, для маловязкой жидкости), то f(x,y,z,t) = 0, и уравнение (6) уп­рощается:

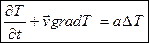. (7)

Второе слагаемое в левой части уравнений (6) и (7) выражает конвективный пе­ре­нос тепла. Если v = 0 (среда неподвижна), то уравнение (6) приобретает вид

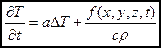. (8)

Это "стандартный" вид уравнения теплопроводности в неподвижной среде. Если тем­пе­ра­ту­ра за­ви­сит только от координаты x (одномерное поле), а функция f = 0, то уравнение (8) принимает вид:

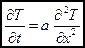. (9)

2 .3. Стационарное температурное поле и тепловой поток через многослойную плоскую стенку. Температурный напор и тер­ми­ческое сопротивление.

1.Постановка задачи и общее решение.

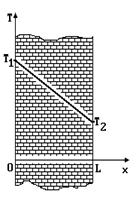
Рассмотрим плоскую стенку (на­при­мер, стену какого-либо здания или сооружения) или плоскую плас­ти­ну из од­нородного материала толщины L. Пусть на одной из сторон этой плас­ти­ны поддерживается температура T₁, а на другой T₂ (см. ри­сунок). Бу­дем счи­тать, что высота и ширина пластины велики по срав­не­нию с ее тол­щи­ной L, и тем­пе­ра­ту­ра в этих направлениях практически не меняется. Для этих ус­ло­вий

; ,

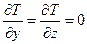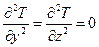и уравнение теплопроводности принимает простейший вид (9) из предыдущего вопроса. Далее, условие ста­ци­о­нар­нос­ти означает, что ¶T/¶t = 0, поэтому

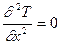, или ,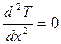

т.к. температура зависит от единственной переменной x. Очевидным решением этого уравнения является

, (1)

T = C₁x + C₂, (2)

где C₁ и C₂ - константы интегрирования, которые должны быть определены из граничных ус­ло­вий. Из по­лу­чен­ного общего решения видно, что в плоской пластине без внутренних источников теп­ла ста­ционарное рас­пределение температуры при граничных условиях любого типа является ли­ней­ным.

2.Граничные условия 1-го и 2-го рода.

Если, как сказано выше, на поверхности плас­ти­ны x = 0 поддерживается температура T₁, а на поверхности x = L - температура T₂, т.е. заданы условия первого рода на обеих поверхностях, то для определения констант интегрирования имеем:

T₁ = C₂,, T₂ = C₁ L + C₂,

откуда C₁ = (T₂ - T₁)/L, и

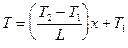, (3)

а плотность теплового потока

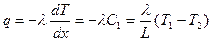. (4)

Последнюю формулу в теплотехнике принято записывать в виде:

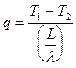. (5)

Эта формула аналогична закону Ома для электрического тока (сила тока равна на­пря­же­нию, деленному на сопротивление данного участка проводника), поэтому разность T₁ - T₂ на­зы­ва­ют тем­пературным напряжением, или температурным напором, величину L/l - теп­ло­вым или тер­ми­ческим сопротивлением, а обратную величину l/L - тепловой про­во­ди­мостью пла­с­ти­ны.

Если на границе х = 0 задано условие второго рода:

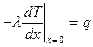, (6)

где q - плотность мощности подводимого к пластине теплового потока, а на границе х = L, как и рань­ше, дано условие первого рода: Т | _x=L = T₂, то получаем следующие значения констант:

C₁ = -q/l, C₂ = T₂ + qL/l,

таким образом,

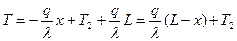. (7)

В частности, температура на границе х = 0 в этом случае равна:

. (8)

3.Граничные условия 3-го рода.

Пусть на обеих поверхностях пластины заданы условия теплообмена с окружающей средой в виде:

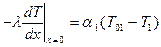, (9)

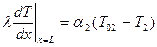, (10)

где T₀₁ и T₀₂ - температура окружающей среды слева и справа от пластины (например, тем­пе­ра­ту­ра воздуха в помещении и на улице); a₁ и a₂ - соответствующие коэффициенты теплообмена.

Подставляя сюда из формул (1) и (2) значения dT/dx = C₁, T₁ = C₂, T₂ = C₁×L + C₂, получаем систему уравнений относительно констант C₁ и C₂:

-lC₁ = a₁ (T₀₁ - C₂),

lC₁ = a₂ (T₀₂ - C₁×L - C₂),

решая которую находим:

, .

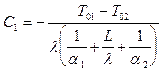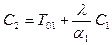Таким образом, распределение температуры внутри пластины имеет вид:

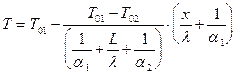, (11)

плотность теплового потока

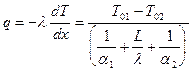, (12)

а тепловое сопротивление

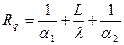. (13)

4.Граничные условия 4-го рода. Поток тепла через многослойную пластину.

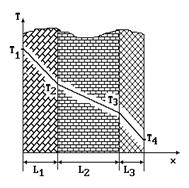
Рассмотрим плоскую стенку, состоящую из нескольких (на­­при­мер, из трех) разнородных, плот­но прилегающих друг к дру­гу слоев, имеющих толщину L₁, L₂, L₃ и теплопроводность l₁, l₂, l₃ со­от­вет­ст­вен­но (см. рисунок). Пусть температуры на­руж­ных по­верх­нос­тей стен­ки T₁ и T₄ заданы. Соприкасающиеся по­верхности слоев имеют тем­пе­ра­ту­ры T₂ и T₃, но значения их за­ранее неизвестны. Тем­пе­ратура и теп­ловой поток при пе­ре­хо­де через соприкасающиеся по­верх­ности ме­­няются непрерывно, в стационарном режиме плотность теп­лового по­­тока q, про­хо­дя­ще­го через каждый слой стен­ки, оди­на­ко­ва по­э­то­му для каж­до­го слоя стенки можно написать:

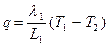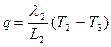, , , (14)

откуда

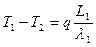, (15)

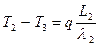, (16)

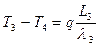. (17)

Складывая (15) - (17), находим:

.

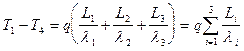Отсюда получаем формулу для плотности теплового потока q, а затем из (14) определяем неизвестные температуры T₂ и T₃:

, (18)

.

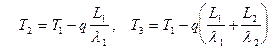Формулу (18) легко обобщить на случай n -слойной стенки и объединить с ре­зуль­та­том, полученным для граничных условий 3-го рода (с формулой (13)): для многослойной стен­ки, состоящей из пластин толщиной L_i с соответствующими коэффициентами тепло­про­водности l_i, тепловое со­про­тив­ле­ние определяется формулой:

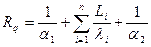. (19)

2.4. Стационарное температурное поле в цилиндрической области. Ста­ци­о­нар­ный тепловой поток через многослойную цилиндрическую стенку.

1.Общее решение и его свойства.

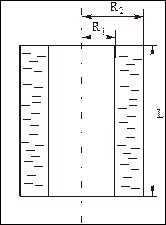
Пусть пространство между двумя коаксиальными ци­линд­ра­ми (тру­бами) с радиусами R₁ и R₂ заполнено неподвижной средой (см. ри­сунок). Будем считать, что длина цилиндров много больше их ра­ди­усов, температура среды зависит только от радиуса r (от рас­сто­я­ния до оси), вдоль z не меняется и от угла j не зависит (в этом случае говорят, что задача является аксиально-сим­мет­рич­ной, или имеет осе­вую симметрию).

Тогда от оператора Лапласа в цилиндрических координатах остается только ра­ди­аль­ная часть; условие ста­­ци­о­нар­ности означает, что ; т.к. температура зависит толь­ко от одной переменной r, то вме­с­то част­ных производных мож­но писать пол­ные производные, и урав­нение теплопроводности при­ни­мает вид:

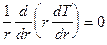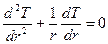, или . (1)

Отсюда ;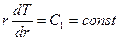

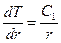; (2)

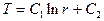, (3)

где C₁ и C₂ - константы интегрирования, которые должны быть определены из граничных условий.

Из полученного общего решения можно сделать два важных вывода.

1). Если область r = 0 не иск­лючена (т.е. если внутренний цилиндр отсутствует, и все прост­ранст­во внутри внешней тру­бы заполнено сплошной средой), то из ис­ход­ного урав­не­ния (1), а также из формул (2) и (3) следует, что константа C₁ должна равняться ну­лю, (иначе про­из­вод­ная dT/dr в точке r = 0 будет бесконечно большой), т.е. должно быть 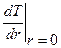= 0. Физически это оз­начает, что температура на оси должна иметь либо мак­си­маль­ное, либо минимальное зна­че­ние, что для осесимметричной задачи совершенно очевидно. Но в этом случае из (3) сле­ду­ет, что T = C₂ = const, т. е. температура во всей области постоянна. Дру­гими словами, если ось r = 0 не исключена, то стационарная задача теплопроводности в ци­линдрической области имеет только тривиальное решение T = const. Подчеркнем еще раз, что этот вывод относится только к стационарному решению.

2). Если пространство, занятое средой, не ограничено (т.е. если внешний цилиндр от­сут­ст­вует, и все прост­ранст­во вокруг внутренней тру­бы заполнено сплошной средой), то из фор­му­лы (3) следует, что константа C₁ должна равняться ну­лю (иначе температура при r ® ¥ будет неограниченно расти), т.е. и в этом случае T = C₂ = const. В частности, если в не­о­гра­ни­чен­ной среде находится источник тепла в форме бесконечно длинной трубы или нити (на­при­мер, проводник с электрическим током), то стационарное распределение температуры никогда не будет достигнуто (оно было бы достигнуто, когда температура всей среды стала бы равной температуре источника тепла, но для неограниченной среды для этого требуется бесконечно большое время). Ниже мы увидим, что для источника тепла сферической формы стационарное распределение температуры существует.

Итак, стационарная осесимметричная задача теплопроводности может иметь не­три­ви­аль­ное решение толь­ко в области 0 < R₁ £ r £ R₂ < ¥.

2.Граничные условия 1-го и 2-го рода.

Пусть поверхности внутреннего и внешнего цилиндров поддерживаются при постоянных температурах T₁ и T₂ соответственно (граничные условия 1-го рода). Тогда, подставляя эти значения в формулу (10.3), получаем систему уравнений

; ,

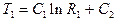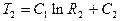решая которую находим константы интегрирования С₁ и С₂:

; .

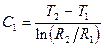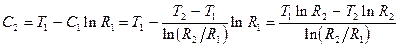Подставляя найденные значения С₁ и С₂ в (3) и (2), получим формулу для ста­ци­о­нар­ного тем­пе­ра­тур­но­го поля в ци­лин­дрической области:

, (4)

и формулу для плотности теплового потока:

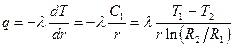. (5)

Теперь рассмотрим задачу с граничным условием 2-го рода. Пусть внутренний цилиндр является нагревателем (например, электро­на­гре­ва­те­лем), и через его поверхность задан по­сто­ян­ный поток тепла:

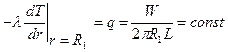, (6)

где W — мощность нагревателя (заданная постоянная величина), а L - его длина. Тем­пе­ра­ту­ра внешнего цилиндра, как и прежде, пусть поддерживается постоянной:

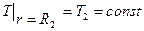, (7)

т.е. на внешней поверхности задано условие 1-го рода.

Подставляя (6) в (2), найдем константу C₁:

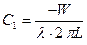, (8)

а затем подставляя (6) и (8) в (3), найдем константу C₂:

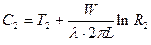. (9)

Таким образом, распределение температуры в пространстве между нагревателем и внеш­ним цилиндром данном случае может быть представлено в следующим образом:

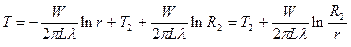, (10)

температура Т₁ на внутреннем цилиндре теперь определится из решения (10):

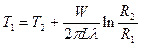, (11)

а плотность потока тепла:

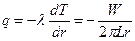. (12)

3.Многослойная цилиндрическая стенка.

Многослойные цилиндрические покрытия на практике применяются довольно часто (на­при­мер, теплоизоляция на трубопроводах теплотрассы и др.). В стационарном режиме ко­ли­чест­во тепла, проходящего через каждый слой, одинаково и постоянно, и расчет термического сопротивления и плотности теплового потока для многослойного ци­линдрического покрытия можно выполнить ана­логично тому, как это было сделано выше для плоской стенки. В ре­зуль­та­те несложных вычислений получаем:

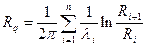, (13)

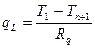, (14)

где q_L - тепловой поток на единицу длины трубы, n - количество слоев, R_i, l_i - внутренний ра­ди­ус и коэффициент теплопроводности i -го слоя, T_n+1 - температура поверхности наружного покрытия.

2.5. Стационарное температурное поле сферического источника тепла в огра­ни­че­нной и в неограниченной среде.

1.Общее решение стационарного уравнения теплопроводности в сферической сис­те­ме координат.

Источники тепла различных конструкций часто применяются как в промышленности, так и в быту. Форму многих из них в первом приближении можно считать сферической. Бо­лее того, тем­пературное поле, создаваемое источником любой формы на расстоянии, много боль­шем чем размеры источника, можно приближенно рассматривать как поле сферического источника теп­ла.

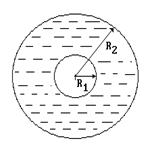
Пусть пространство между двумя коаксиальными сферами с ра­­ди­у­са­ми R₁ и R₂ заполнено не­подвижной средой (см. рисунок). Бу­дем счи­тать, что температура среды зависит только от рас­стояния до на­чала ко­ординат и не зависит от углов j и q (в этом случае говорят, что тем­пе­­ра­турное поле сферически-симметрично, или имеет цент­раль­ную сим­метрию). Тогда от опе­ра­то­ра Лапласа остается только ра­­ди­альная часть, и ста­ци­о­нар­ное (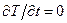) одно­мер­ное уравнение теп­­ло­­про­вод­нос­ти в сферических координатах принимает вид:

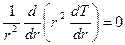. (1)

Интегрируя (1), получаем:

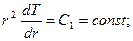(2)

отсюда 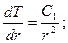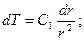(3)

интегрируя вторично получаем общее решение:

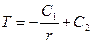, (4)

где C₁ и C₂ - константы интегрирования, которые должны быть определены из граничных ус­ло­вий.

Из общего решения, а также из формул (3) следует, что если область r = 0 не иск­лю­че­на (т.е. если внутренняя сфера отсутствует и все пространство внутри внешней сферы за­пол­не­но сплошной средой), то так же, как и в цилиндрической системе координат, должно быть:

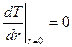, т. е. , ,

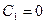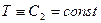т. е. в этом случае стационарное решение возможно лишь когда температура во всей области по­стоянна (тривиальное решение).

Однако, если пространство, занятое средой, не ограничено (т.е. если внешняя сфера от­сут­ствует, и все пространство вокруг внутренней сферы заполнено сплошной средой), то, в от­ли­чие от цилиндрической системы координат, при r ® ¥ температура остается огра­ни­чен­ной; это означает, что для источника тепла сферической формы в безграничной среде не­три­ви­аль­ное стационарное решение су­щест­ву­ет (см.ниже формулу (7)).

2. Температурное поле в ограниченной среде; условие 1-го рода.

Если область r = 0 исключена, т. е. если ищется температурное поле в области 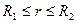, то должны быть заданы граничные условия на сферах 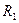и .

Пусть на обеих сферах поддерживаются постоянные температуры 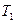и 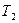(т.е. заданы ус­ло­вия 1-го рода):

; .

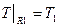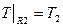Тогда ; ,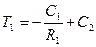

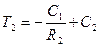и решая эту систему уравнений относительно 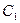и 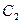, находим:

;

.

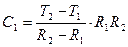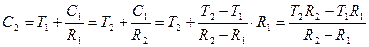Итак,

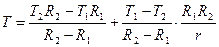. (5)

3.Температурное поле в ограниченной среде; условие 2-го рода на внутренней сфере.

Пусть теперь внутренняя сфера представляет собой нагреватель мощности W, а на внеш­ней сфере по-прежнему задана постоянная температура T₂. Тогда гра­нич­ные условия имеют вид:

; .

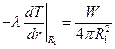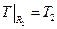Из формулы (3) 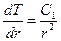находим: 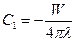. Подставляя в общее решение (4), оп­ре­де­ляем вторую константу интегрирования:

.

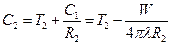Таким образом:

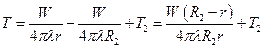. (6)

В частности, температура внутренней сферы равна

.

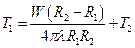4.Температурное поле в неограниченной среде.

Пусть сферический нагреватель радиуса R₁ и мощностью W находится в неогра­ни­чен­ной сре­де, температура которой вдали от источника равна Т₀. Тогда граничные условия можно за­пи­сать в виде:

; .

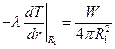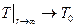Используя формулу (3) и общее решение (4), находим константы интегрирования:

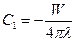; T₀=C₂.

Таким образом, стационарное поле сферического источника тепла в неограниченной не­под­виж­ной среде имеет вид:

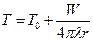. (7)

В частности, температура на поверхности источника:

,

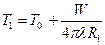где R₁ - радиус источника.

Date: 2015-05-09; view: 2571; Нарушение авторских прав