Термодинамики

Уравнение первого закона термодинамики (2.27) обычно записывается с расположением теплоты в левой части, а изменения внутренней энергии и работы расширения в правой:

Q = U₂ - U₁ + L'. (2.29)

Для одного килограмма вещества оно примет вид

q = u₂ - u₁ + l'. (2.30)

Это интегральная форма записи первого закона термодинамики, т.е. целиком для всего процесса, происходящего с веществом от состояния 1 до состояния 2.

Дифференциальная форма записи первого закона термодинамики, будет иметь вид

¶Q = dU + ¶L', (2.31)

¶q = du + ¶l'. (2.32)

В этих уравнениях величинами L' и l' обозначается работа изменения объема, совершаемая телом в реальных необратимых процессах. Работа расширения увеличивает механическую энергию системы, т.е. она может передаваться или внешнему потребителю работы, или внешней среде.

При обратимых процессах вся работа изменения объема тела затрачивается на преодоление внешнего давления и аккумулируется системой в форме механической энергии. Расчетное выражение работы изменения объема обратимого процесса было получено ранее в виде

¶l = Pdv.

При необратимых процессах изменения объема тела имеет место трение. Например, трение газа о стенки емкости или расширение газа идет с образованием вихревого движения. Трение приводит к увеличению внутренней энергии тела (оно нагревается). Поэтому внешняя работа расширения оказывается меньше работы изменения объема обратимого процесса на величину работы трения:

¶l' = ¶l - ¶l_тр = Pdv - ¶l_тр. (2.33)

Здесь ¶l и ¶l' – работа обратимого и необратимого процессов;

¶l_тр – работа трения.

Работа трения ¶l_тр переходит в конечном результате в теплоту трения dqтр. Тогда первый закон термодинамики для необратимого процесса расширения тела можно записать в виде

¶q = du + ¶l - ¶l_тр = du + ¶l - ¶q_тр,

перегруппировав члены данного уравнения, окончательно получим

¶q* = ¶q + ¶q_тр = du + ¶l= du + pdv, (2.34)

где ¶q* – полная теплота, полученная телом в необратимом процессе.

Для обратимых процессов ¶q_тр=0, и первый закон термодинамики обратимого процесса будет иметь вид

¶q = du + ¶l = du + pdv. (2.35)

Поскольку внутренняя энергия может быть представлена в виде функции любой пары независимых параметров состояния (она сама параметр состояния), то выражение (2.35) можно записать в виде частных производных от этих параметров состояния. Например, выразив du в частных производных от P и v, получим выражения

du = (¶u/¶p)_vdp + (¶u/¶v)_pdv, (2.36)

¶q = (¶u/¶p)_vdp + [(¶u/¶v)_p + p]dv. (2.37)

Таких уравнений можно записать столько, сколько существует пар независимых параметров состояния. Значение дифференциальных уравнений первого закона термодинамики очень велико, поскольку, зная функциональную взаимосвязь термических параметров состояния вещества (Р,v,T), используя эти дифференциальные уравнения, можно рассчитать энергетические параметры данного вещества (u, s и т.п.) и его теплоемкости, а также решать и обратную задачу.

2.4.2. Энтальпия

Многие термодинамические расчеты облегчаются при использовании аддитивных свойств термодинамических тел, называемых энергетическими или калорическими параметрами состояния. Такое название эти параметры состояния получили потому, что в их единицах измерения присутствует величина энергии (Дж) или (ккал). С некоторыми из них мы уже познакомились: это энтропия S(Дж/К) и внутренняя энергия U(Дж). Теперь познакомимся с энтальпией.

Преобразуем выражение первого закона термодинамики (2.35), записав его в виде

¶q=du+Pdv=du+d(Pv)-vdP=[d(Pv)=vdP+Ppdv]=d(u+Рv)-vdp. (2.38)

В равенстве (2.38) сумма (u + Рv) является функцией состояния или параметром состояния, ее назвали энтальпией и обозначили буквой h:

h = u + Рv. (2.39)

В выражении (2.39) h – удельная энтальпия, для всей массы тела полная энтальпия обозначается буквой H и рассчитывается как

H = mh = U + РV. (2.40)

Полная энтальпия H обладает свойствами аддитивности (суммирования), т.к. внутренняя энергия U и объем V – величины экстенсивные, а давление Р – величина интенсивная. Удельная энтальпия h обладает свойствами интенсивной величины. Энтальпия относится к энергетическим (калорическим) параметрам.

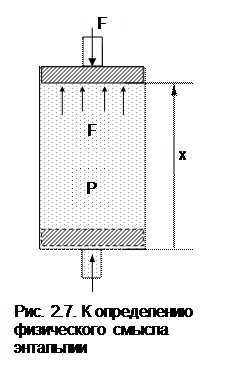Энтальпия имеет определенный физический смысл [7]. Прокоментируем физический смысл энтальпии с помощью рис. 2.7. В цилиндре с поршнем находится газ при давлении Р. Силовое воздействие давления газа на поршень уравновешивается внешним силовым воздейсвием F, т.е. система находится в равновесном состоянии. Энергию газа такой системы можно представить в виде суммы двух энергий: внутренней энергии газа – U и потенциальной энергии газа, которая характеризуется работой внешних сил, уравновешивающих давление газа, затраченных на заполнение газом данного объема.

Получение потенциальной энергии газом может быть проиллюстрировано в виде работы внешних сил, затраченной на перемещение поршня в цилиндре, в случае заполнения его газом при постоянном давлении от нулевого объема V=0 до объема V. Поскольку при заполнении газом цилиндра над газом со стороны окружающей среды была совершена работа, то энергия газа увеличилась на величину этой работы. Это потенциальная энергия давления газа, которая рассчитывается как произведение внешней силы F на перемещение поршня x или как произведение давления газа на изменение его объема от 0 до V:

Fx = P(V - 0) = PV.

В итоге получили, что полная энергия такой системы есть сумма U+PV, а это и есть энтальпия H=U+PV.

Таким образом, энтальпия есть полная энергия расширенной системы, представляющяя сумму внутренней энергии и внешней – потенциальной энергии давления.

Как любой параметр состояния, энтальпия может быть определена любой парой независимых параметров состояния.

Используя понятие энтальпии, первый закон термодинамики можно записать в виде

¶q = dh - vdР, (2.41)

¶Q = dH - VdР. (2.42)

Из выражения (2.41) видно, что энтальпией удобно пользоваться при определении теплоты в изобарных процессах (Р=const): ¶q_p=dh_р.

Изобарная теплоемкость тела тоже может быть рассчитана с использованием величины изменения энтальпии:

с_p = ¶q_p/dT = (¶h/¶T)_p. (2.43)

Необходимо обратить внимание на то, что выражение (2.43) справедливо только для изобарных процессов, т.е. разность энтальпий можно рассчитать как произведение изобарной теплоемкости на изменение температуры только при Р=const: dh_p=c_pdT. В общем случае изменение энтальпии можно представить как полный дифференциал, выраженный через частные производные энтальпии от любой пары независимых параметров состояния. Например, выразим изменение энтальпии через ее зависимость от давления и температуры:

dh = (¶h/¶T)_pdT + (¶h/¶P)_TdP, (2.44)

используя выражение (2.43) для первого слагаемого, получим

dh = c_pdT + (¶h/¶P)_TdP. (2.45)

При определении энтальпии, как и для внутренней энергии, выбирают начало отсчета. Хотя выбор параметров начала отсчета энтальпии произволен, т.к. в термодинамике важно не абсолютное ее значение, а разность, необходимо иметь в виду, что начала отсчета и внутренней энергии, и энтальпии связаны между собой. Так, если u_о = 0, то при тех же условиях h_о = Р_оv_о > u_о.

В практике широко используется диаграмма h, s. Для нее начала отсчета энтальпии и энтропии выбираются при одинаковых параметрах состояния. С использованием h, s- диаграммы, легко графически представляются и рассчитываются основные процессы в теплоэнергетике: изобарный, адиабатный, а также оцениваются необратимости на трение и дросселирование.

Date: 2015-05-09; view: 897; Нарушение авторских прав