Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Внутренняя энергия идеального газа
|
|
Исходя из определения идеального газа в нем отсутствует потенциальная составляющая внутренней энергии (отсутствуют силы взаимодействия молекул, кроме ударного). Таким образом, внутренняя энергия идеального газа представляет собой только кинетическую энергию движения его молекул. Ранее (уравнение (1.10)) было показано, что кинетическая энергия поступательного движения молекул газа прямо пропорциональна его абсолютной температуре:
.
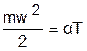Используя выражение универсальной газовой постоянной (3.6), можно определить величину константы a:
.
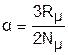Таким образом, кинетическая энергия поступательного движения одной молекулы идеального газа будет определяться выражением
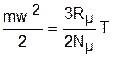. (3.10)
В соответствии с кинетической теорией распределение энергии по степеням свободы равномерное. У поступательного движения 3 степени свободы. Следовательно, на одну степень свободы движения молекулы газа будет приходитья 1/3 ее кинетической энергии:
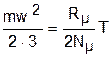. (3.11)
Для двух, - трех - и многоатомных молекул газа кроме степеней свободы поступательного движения есть степени свободы вращательного движения молекулы (рис.3.1). Для двухатомных молекул газа число степеней свободы вращательного движения равно 2, для трех - и многоатомных молекул – 3.
Поскольку распределение энергии движения молекулы по всем степеням свободы равномерное, а число молекул в одном киломоле газа равняется Nm, внутреннюю энергию одного киломоля идеального газа можно получить, умножив выражение (3.11) на число молекул в одном киломоле и на число степеней свободы движения молекулы данного газа:
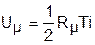, (3.12)
где Um – внутренняя энергия 1 киломоля газа, Дж/кмоль;
i – число степеней свободы движения 1 молекулы газа.
Для 1-атомного газа i = 3, для 2-атомного газа i = 5, для 3-атомного и многоатомного газов i = 6.
 |
Для многоатомного газа i=6, так как существуют 3 степени свободы поступательного движения и 3 степени свободы вращательного движения молекул. Может быть еще колебательное движение атомов в молекуле, но его обычно учитывают для реальных газов, используя экспериментальные данные. Для идеальных газов колебательное движение атомов в молекулах тоже может быть учтено при расчете внутренней энергии (см. в разд. 4.6). На данном этапе изложения материала будем руководствоваться молекулярно-кинетичесой теорией идеального газа. В соответствии с ней атомы в молекулах идеального газа имеют жесткие связи, т.е. колебательного движения атомов в молекулах нет.
Для одного килограмма идеального газа удельная внутренняя энергия (Дж/кг) определяется делением выражения (3.12) на молярную массу газа:
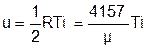. (3.13)
Для произвольного количества газа внутренняя энергия определяется как произведение его массы на удельную внутреннюю энергию этого газа:
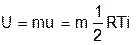, (3.14)
где m – масса газа, кг;
U – полная внутрення энергия идеального газа.
Если система состоит из нескольких различных по физическим свойствам газов, то, подчиняясь закону сложения (аддитивности), его полная внутренняя энергия будет определяться суммой внутренних энергий компонентов газовой смеси:
U = m1u1 + m2u2 + ××× + mnun, (3.15)
где n – число компонентов газа в системе.
Полученные уравнения внутренней энергии идеального газа (3.12) – (3.15) указывают на то, что внутренняя энергия идеального газа зависит только от абсолютной температуры газа и числа степеней свободы движения его молекул:
u = f(T) или (du/dP)T = 0, (du/dv)T = 0. (3.16)
Date: 2015-05-09; view: 1103; Нарушение авторских прав