
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теплоемкости процессов
|
|
Поскольку теплота является функцией процесса, то и теплоемкость есть функция процесса. На практике наибольшее применение нашли теплоемкости изобарного – cp при Р=const и изохорного – cv при v=const процессов.
Теплоемкости идеальных газов
Воспользуемся первым законом термодинамики для получения аналитических выражений изохорной и изобарной теплоемкостей идеальных газов:
c = ¶q/dT = du/dT + ¶l/dT = du/dT + Pdv/dT. (3.21)
При v=const (dv=0) из выражения (3.21) получим аналитическое выражение для изохорной теплоемкости:
сv = (du/dT)v. (3.22)
Подставив сv в выражение дифференциала внутренней энергии при независимых переменных T и v, получим выражение
du = (du/dT)vdT + (du/dv)Tdv = cvdT + (du/dv)Tdv. (3.23)
Для идеального газа внутренняя энергия – функция только одного термического параметра – температуры, т.е. (du/dv)T=0. Следовательно, для идеального газа выражение (3.23) примет вид
du = cvdT. (3.24)
Аналитическое выражение изохорной теплоемкости идеального газа получается из (3.24) и выражения внутренней энергии идеального газа:
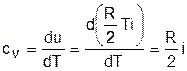 . (3.25)
. (3.25)
Из выражения (3.25) следует, что изохорная теплоемкость идеального газа величина постоянная.
Подставив выражение изохорной теплоемкости идеальных газов (3.25) в уравнение (3.21), получим выражение теплоемкости идеального газа в виде
c = cv + Pdv/dT. (3.26)
Рассмотрим выражение (3.26) применительно к идеальному газу для изобарного процесса P=const. Второе слагаемое выражения (3.26) для идеального газа при P=const можно получить дифференцированием уравнения Менделеева – Клапейрона:
Pv=RT, при Р=const Pdv=RdT ® Pdv/dT=R.
В результате этих преобразований получаем расчетное выражение для изобарной теплоемкости идеального газа:
cp = cv + R. (3.27)
Уравнение (3.27) носит название формула Майера. Используя формулу Майера, получим аналитическое выражение изобарной теплоемкости идеального газа:
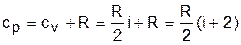 . (3.28)
. (3.28)
Изобарная теплоемкость идеального газа больше изохорной теплоемкости на величину газовой постоянной.
Аналитические выражения для удельных мольных и объемных изохорных и изобарных теплоемкостей идеального газа легко получить, используя их взаимосвязь с удельными массовыми теплоемкостями (3.25) и (3.28):
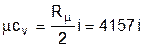 Дж/(кмоль×К); (3.29)
Дж/(кмоль×К); (3.29)
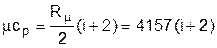 Дж/(кмоль×К); (3.30)
Дж/(кмоль×К); (3.30)
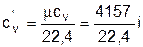 , Дж/(нм3×К); (3.31)
, Дж/(нм3×К); (3.31)
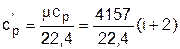 Дж/(нм3×К). (3.32)
Дж/(нм3×К). (3.32)
В соответствии с молекулярно-кинетической теорией идеальных газов их изобарные и изохорные теплоемкости (выражения (3.25), (3.28) – (3.32)) – величины постоянные, не зависящие от термических параметров состояния газа.
В системе единиц, основанной на калории (1ккал=4187кДж) мольная теплоемкость идеального газа определяется простым соотношением (ккал/(кмоль×К)):
mcv» i; (3.33)
mcp» (i+2). (3.34)
Теплоемкость реальных газов
Для реальных газов теплоемкости cv и сp зависят от давления и температурыгаза. Это обусловлено наличием сил межмолекулярного взаимодействия, изменением взаимного положения атомов в молекулах (молекулы двух - и многоатомных газов не жесткие, присутствует колебательное движение атомов в молекуле) и неравномерным распределением внутренней энергии по степеням свободы в зависимости от изменения температуры и давления газа.
 Зависимость теплоемкости газов от давления в большей степени проявляется в состоянии газов, близком к области насыщения (см. разд. 6). Для газов, состояние которых далеко от области насыщения, зависимость теплоемкости от давления незначительна и при практических расчетах ею пренебрегают. Зависимость от температуры очень существенна, ей пренебрегать при точных расчетах нельзя.
Зависимость теплоемкости газов от давления в большей степени проявляется в состоянии газов, близком к области насыщения (см. разд. 6). Для газов, состояние которых далеко от области насыщения, зависимость теплоемкости от давления незначительна и при практических расчетах ею пренебрегают. Зависимость от температуры очень существенна, ей пренебрегать при точных расчетах нельзя.
Аналитическое выражение этой зависимости весьма сложное и требует нахождения целого ряда экспериментальных констант для каждого газа. Практическое определение теплоемкостей сv и сp реальных газов ведется экспериментально. В соответствии с этим были введены понятия истинной и средней теплоемкости газа.
Истинная теплоемкость газа соответствует расчетному выражению
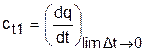 , (3.35)
, (3.35)
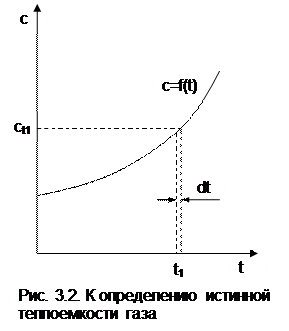
она определяется как частное от деления элементарной теплоты процесса на элементарное изменение его температуры относительно точки процесса с фиксированной температурой (рис.3.2). Для реальных газов каждому значению температуры процесса соответствует вполне определенное значение истинной теплоемкости.
Экспериментальная зависимость истинной теплоемкости процесса реального газа от температуры обычно представляется в виде степенного полинома графика (см. рис.3.2) или табличного численного материала.
с = а + b1t + b2t2 + b3t3 + ×××× + bntn. (3.36)
Определение теплоты с помощью истинной теплоемкости ведется интегрированием:
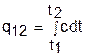 . (3.37)
. (3.37)
Теплота q12 на рис.3.3 соответствует площади под процессом 12. Средняя теплоемкость газа соответствует расчетному выражению
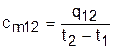 , (3.38)
, (3.38)
она определяется как теплота процесса, идущего в интервале температур t1 и t2, деленная на разность этих температур (рис.3.3).
Средней теплоемкостью можно пользоваться только на данном интервале температур. Это очень неудобно, т.к. для практических расчетов необходимо в таблицах экспериментальных данных по средним теплоемкостям предусмотреть все возможные температурные интервалы. Выход из этой ситуации был найден введением средней теплоемкости, определенной от одинаковой начальной температуры. В качестве такой температуры приняли 0 оС. Расчетное выражение средней теплоемкости, определенной от 0 оС, имеет вид
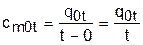 . (3.39)
. (3.39)
Используя эту теплоемкость, можно определить теплоту и среднюю теплоемкость в любом интервале температур процесса (рис.3.3). Площадь под процессом А1 соответствует теплоте q01=cm01t1, а под процессом А2 – теплоте q02=cm02t2, теплота процесса 12 определяется как разность этих площадей:
q12 = q02 - q01 = cm02t2 - cm01t1. (3.40)
Следовательно, средняя теплоемкость на интервале температур t1 и t2 будет определяться как
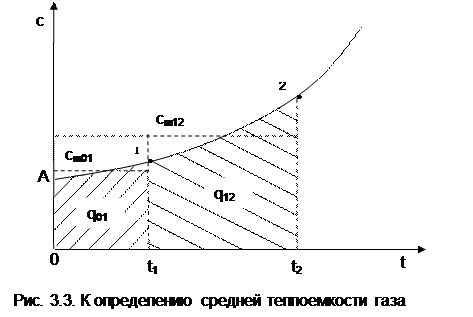 |
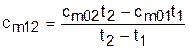 . (3.41)
. (3.41)
В справочных таблицах свойств газов даются значения истинных теплоемкостей при конкретных температурах и средних теплоемкостей в интервале от 0 до t оС. Экспериментально проще определяются изобарные теплоемкости газов. Изохорные теплоемкости газов, подчиняющихся уравнению Pv=RT, рассчитывают по формуле cv=cp-R (Майера). Удельные мольные и объемные теплоемкости реальных газов рассчитываются по их соотношениям с удельными массовыми теплоемкостями.
Отношение изобарной и изохорной теплоемкостей
При расчетах газовых процессов часто используется коэффициент, представляющий отношение изобарной и изохорной теплоемкостей газов:
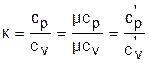 . (3.42)
. (3.42)
Этот коэффициент носит название коэффициента Пуассона. Для идеальных газов с постоянными темлоемкостями сp и сv это величина постоянная:
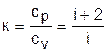 , (3.43)
, (3.43)
для одноатомных газов i=3, к=5/3=1,667;
для двухатомных i=5, к=7/5=1,4;
для многоатомных i=6, к=8/6=1,333.
Для реальных двух - и многоатомных газов, подчиняющихся уравнению Pv=RT, коэффициент Пуассона так же, как и теплоемкости, зависит от температуры. С повышением температуры у них к уменьшается, это следует из зависимости
к= cp/cv = (cv + R)/cv = 1 + R/cv, (3.44)
поскольку с увеличением температуры изохорная теплоемкость реального газа увеличивается.
Date: 2015-05-09; view: 2429; Нарушение авторских прав