Смеси идеальных газов. Смеси идеальных газов являются также идеальными газами и подчиняются уравнению состояния идеальных газов (уравнению Клапейрона)

Смеси идеальных газов являются также идеальными газами и подчиняются уравнению состояния идеальных газов (уравнению Клапейрона)

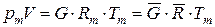, (209)

где 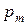, 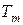– давление и температура смеси.

Средняя температура и среднее давление смеси характеризуют конечное состояние диффузионного равновесия смеси.

Состояние компонентов смеси в процессе перемешивания непрерывно изменяется, начиная с момента первичного выравнивания давлений компонентов и кончая состоянием диффузионного равновесия, когда давление каждого из компонентов снижается до уровня стабильного парциального давления .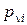

Закон диффузионного равновесия смеси идеальных газов (закон Дальтона) характеризует установившееся состояние газовой смеси и формулируется следующим образом: каждый компонент смеси ведет себя в газовой смеси так, как будто он один при температуре смеси 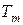равномерно распространен во всем объеме смеси и развивает при этом давление, которое называется парциальным .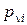

Уравнения состояния для i -го компонента и всей смеси идеальных газов могут быть представлены в следующем виде:

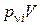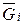
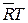= ; (210)

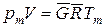. (211)

При делении уравнения (210) на уравнение (211) получаем

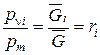. (212)

Из соотношения (212) следует, что парциальное давление i -го компонента 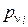в смеси идеальных газов определяется через полное давление смеси 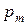и молярную концентрацию компонента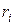

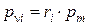. (213)

После преобразования соотношения (213) получаем, что сумма парциальных давлений всех компонентов смеси идеальных газов равна полному давлению смеси

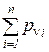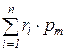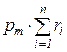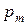= = = . (214)

Поскольку внутренняя энергия и энтальпия идеального газа - функции только температуры, исходными соотношениями для определения средней температуры смеси идеальных газов 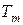служат следующие соотношения:

в схеме смешения при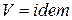

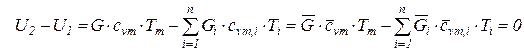; (215)

в схеме смешения при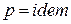

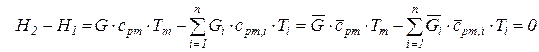. (216)

С учетом этих соотношений (215), (216) получаем обобщенное выражение по определению средней температуры смеси идеальных газов 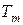для различных схем смешения

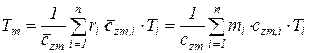, (217)

где 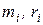– массовая и молярная концентрации i- го компонента смеси; 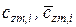– средние удельные массовая и молярная теплоемкости i- го компонента смеси в процессах 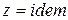(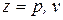); 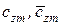– средние удельные массовая и молярная теплоемкости смеси,

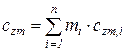, (218)

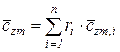. (219)

Объемная концентрация каждого компонента в смеси 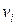определяется как отношение приведенного объема v_i,пр компонента при давлении и температуре смеси к объему всей смеси v при тех же условиях

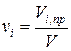. (220)

Для идеального газа, исходя из уравнения состояния

v_i,пр = 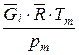, v = . (221)

После подстановки v_i,пр и V в соотношение (220) получаем

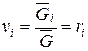. (222)

Отсюда следует, что для смесей идеальных газов объемная и молярная концентрации компонентов численно равны.

Date: 2015-05-09; view: 659; Нарушение авторских прав