Математическое выражение второго начала термодинамики

Наиболее наглядно принцип возрастания энтропии доказывается на основе изучения круговых процессов тепловых машин.

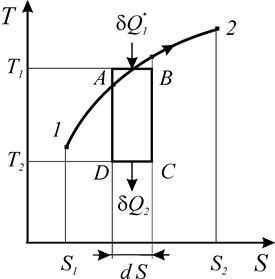
Рассмотрим реальный процесс 1-2 на диаграмме Т-S (рис. 17).

Выделим на кривой процесса элементарный участок А-В и к нему добавим три обратимых процесса: адиабату расширения В-С, изотерму отвода теплоты С-D и адиабату сжатия D-А. Полученный цикл А-В-С-D, в целом, необратим из-за реального процесса 1-2, а следовательно его КПД меньше, чем у цикла Карно

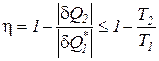. (182)

В выражении (182) справедлив знак неравенства, если рассматриваемый цикл (А-В-С-D) необратим, и знак равенства, если рассматривается обратимый цикл.

После преобразования выражения (182), для любых циклов получаем:

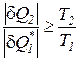; (183)

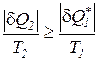; (184)

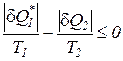. (185)

Учитывая то, что количество теплоты, подведенной к рабочему телу извне, имеет положительный знак (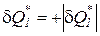), а количество теплоты,
отведенной от рабочего тела – отрицательно (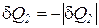), из
выражения (185) получаем следующее неравенство

. (186)

Для рабочего тела в обратимом процессе CD согласно II началу термостатики

. (187)

Согласно условию замыкания кругового процесса (A-B-C-D-A), интегральное изменение любой функции состояния рабочего тела равно нулю, а, так как энтропия изменяется только в процессах A-B и C-D, это условие можно представить следующим образом:

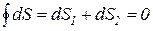. (188)

Выражение (186) с учетом соотношений (187), (188) приобретает следующий вид:

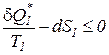(189)

или

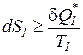. (189а)

Вследствие того, что при выводе рассматривался произвольный процесс и не было ограничений на свойства рабочего тела, результаты вывода (выражение 189а) имеют самый общий характер.

Итоговое математическое выражение второго начала термодинамики в дифференциальной и интегральной формах, как принципа возрастания энтропии изолированных систем имеет следующий вид:

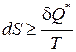; (190)

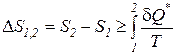. (191)

Знак неравенства в выражениях (190), (191) справедлив в случае, когда в системе происходят реальные необратимые процессы, а равенства – при протекании обратимых процессов.

Если совместить математические выражения второго начала термостатики (162) и второго начала термодинамики (190) то получается следующее соотношение:

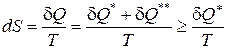, (192)

из которого вытекает следующее утверждение:

dS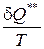^** = > 0, (193)

а при условии, что абсолютная температура всегда положительна (T > 0), непосредственно следует принцип необратимости внутреннего теплообмена

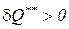. (194)

Данное неравенство (194) свидетельствует о том, что внутренний теплообмен d Q^** в реальных процессах имеет только положительный знак, т.е. работа и количество теплоты в действительных процессах всегда меньше работы и теплоты в обратимом процессе. Затраты работы на необратимые потери в реальных процессах, равные количеству теплоты внутреннего теплообмена 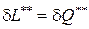, однозначно способствуют росту энтропии.

Для изолированной системы,у которой отсутствует теплообмен с окружающей средой (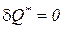), неравенства (190), (191) принимают вид

dS_изол ³ 0, S₂ ³ S₂. (195)

Анализ выражения (195) наглядно показывает, что какие бы процессы не протекали в изолированной системе, ее энтропия не может уменьшаться. При протекании в изолированной системе необратимых процессов энтропия системы возрастает; если же в ней протекают обратимые процессы, то энтропия системы остается неизменной.

Из анализа математического выражения второго начала термодинамики (191) следует, что в том случае, когда в изолированной системе протекают самопроизвольные процессы, сопровождающиеся выравниванием температуры различных ее частей, энтропия системы увеличивается. Отсюда следует, что энтропия является величиной, определяющей близость изолированной системы к состоянию равновесия.

Все реальные процессы, происходящие в природе, необратимы и сопровождаются частичным переходом различных видов энергии в теплоту, которая рассеивается в пространстве. Обратный же переход теплоты в другие виды энергии возможен только при наличии разности температур.
Р. Клаузиус ввел энтропию как меру «деградации» энергии. Направленность протекания процессов во Вселенной, по версии Клаузиуса, должна привести к тепловому равновесию, из которого Вселенная выйти самостоятельно не может. Состояние Вселенной, при котором в ней устанавливается тепловое равновесие, было названо состоянием «тепловой смерти Вселенной».

Следует отметить, что свои выводы Р. Клаузиус сделал, рассматривая Вселенную как изолированную систему. Современная наука опровергает это предположение. Кроме того, математическое выражение второго начала термодинамики и разнообразие процессов, протекающих во Вселенной, не исключают возможности существования процессов, имеющих отрицательный знак внутреннего теплообмена (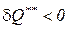). Эти обстоятельства подвергают сомнению правомерность теории Р. Клаузиуса о «тепловой смерти Вселенной».

Date: 2015-05-09; view: 881; Нарушение авторских прав