Простейшие термодинамические процессы

Простейшими термодинамическими процессами обычно считают изобарный, изохорный и изопотенциальные процессы.

Изобарный процесс (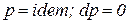) – процесс в котором давление в системе остается постоянным.

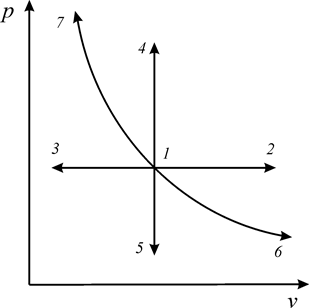
Изобарный процесс (или изобара) графически представлен на рис. 5.

В изобарных процессах происходит увеличение (1-2) или уменьшение (1-3) удельного объема, что связано изменением температуры, обусловленным подводом или отводом теплоты.

Изобарные процессы подвода или отвода теплоты происходят в поршневых двигателях внутреннего сгорания, газотурбинных, паросиловых, холодильных установках и др.

Для идеального газа в изобарном процессе (1-2) значение удельного объема прямо пропорционально температуре рабочего тела .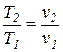

Удельная термодинамическая и потенциальная работы в изобарном процессе определяются из соотношений

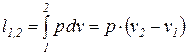, (79)

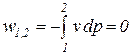. (80)

Количество теплоты, подведенной к рабочему телу или отведенной от него в изобарном процессе, определяется из выражения первого начала термодинамики

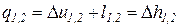. (81)

Изохорный процесс (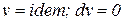) – процесс, при котором объем системы или удельный объем рабочего тела остается постоянным (рис. 5).

В изохорных процессах происходит увеличение (1-4) или уменьшение (1-5) давления, что связано с соответственным изменением температуры – подводом или отводом теплоты.

Изохорные процессы подвода или отвода теплоты происходят в поршневых двигателях внутреннего сгорания, газотурбинных, паросиловых установках и др.

Для идеального газа в изохорном процессе (1-4) давление прямо пропорционально температуре рабочего тела .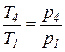

Удельная термодинамическая и потенциальная работы в изохорном процессе определяются из соотношений

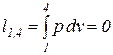, (82)

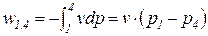. (83)

Количество теплоты, подведенной к рабочему телу или отведенной от него в изохорном процессе, определяется из выражения первого начала термодинамики

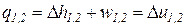. (84)

Изопотенциальный процесс – термодинамический процесс изменения состояния системы, при котором значение потенциальной
функции () сохраняет неизменное значение
(процессы 1-6, 1-7) (рис. 5).

Для идеального газа, согласно уравнению Клапейрона (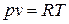), изопотенциальный процесс (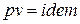) является и изотермическим ().

Удельная термодинамическая и потенциальная работы в изопотенциальном процессе (1-6) определяются из следующих соотношений:

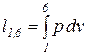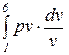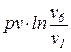= = ; (85)

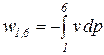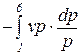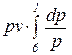= = = . (86)

Нетрудно заметить, что постоянство потенциальной функции (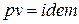) приводит к равенству логарифмов в выражениях (85) и (86) в силу того, что соблюдается условие 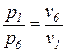. Поэтому, в изопотенциальном процессе численные значения термодинамической и потенциальной работ равны между собой.

Количество теплоты, подведенной к рабочему телу или отведенной от него в изопотенциальном процессе определяется из выражения первого начала термодинамики по балансу рабочего тела

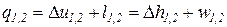. (87)

Уравнения перечисленных простейших и любых других термодинамических процессов могут быть представлены одним уравнением. Это уравнение называется уравнением политропы, а термодинамические процессы, описываемые этим уравнением, называются политропными.

Date: 2015-05-09; view: 1011; Нарушение авторских прав