Закон Майера. Энтропия идеального газа

Идеальные газы подчиняются уравнению состояния Клапейрона 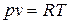и закону Джоуля, согласно которому удельная внутренняя энергия идеального газа зависит только от температуры

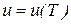. (64)

Совместное использование уравнения Клапейрона и закона Джоуля приводит к выводу о том, что удельная энтальпия идеального газа также являются функциями только температуры

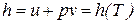. (65)

С учетом законов идеальных газов и исходя из соотношений (55), (56), изменение внутренней энергии 1 кг идеального газа в элементарном и конечном (1-2) процессах находится по следующим формулам:

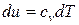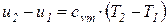; , (66)

а изменение энтальпии 1 кг идеального газа в элементарном и конечном (1-2) процессах определяется по следующим зависимостям:

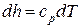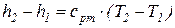; . (67)

После подстановки соотношений (66) и (67) в выражение первого начала термодинамики для простых тел (48), (49) получаем уравнение первого начала термодинамики для идеального газа по балансу рабочего тела в дифференциальной и интегральной формах:

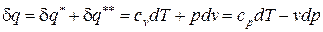; (68)

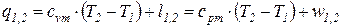. _. (69)

Из уравнения первого начала термодинамики для идеального газа (68) можно получить следующее выражение:

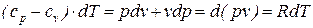, (70)

из которого следует, что разность истинных теплоемкостей идеального газа при постоянном давлении и при постоянном объеме равна величине характеристической газовой постоянной

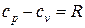. (71)

Это выражение (71) впервые было получено Р. Майером (1842 г.) и называется законом Майера.

Уравнение (71) может быть записано и для одного кмоля газа

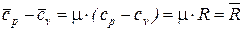. (72)

Разделив уравнение (68) на абсолютную температуру T, получим

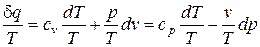. (73)

С учетом того, что для идеального газа, исходя из уравнения Клапейрона, справедливы равенства: 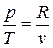; 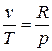получим

. (74)

Правая часть уравнения (74) представляет собой сумму полных дифференциалов. Это значит, что и соотношение 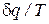есть полный дифференциал некоторой функции состояния идеального газа (s), называемой удельной энтропией.

Изменение удельной энтропии в элементарном процессе представляет собой полный дифференциал и определяется соотношением

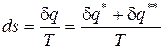. (75)

Из уравнения (74) после интегрирования получим, что изменение удельной энтропии идеального газа в процессе (1-2) может быть найдено из соотношения

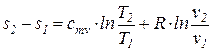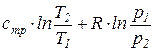= . (76)

Теплоемкост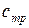и и называются вторыми средними теплоемкостями и находятся путем осреднения по логарифму абсолютных температур

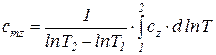. (77)

Если принять, что истинная теплоемкость является линейной функцией температуры 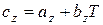, то

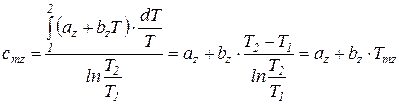. (78)

Таким образом, первая средняя теплоемкость равна истинной теплоемкости при средней арифметической температуре процесса (T_ma), а вторая – при средней логарифмической температуре процесса (T_mz). В случае, если 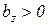, то первая средняя теплоемкость численно несколько больше второй.

5. Процессы изменения состояния термодинамических систем

Date: 2015-05-09; view: 737; Нарушение авторских прав