Первое начало термодинамики для простых тел

Для простых тел, то есть систем, состояние которых определяется двумя независимыми переменными, термодинамическая работа определяется как 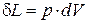и математическое выражение первого начала термодинамики в дифференциальной форме примет следующий вид:

для термодинамической системы

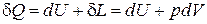; (42)

для 1 кг системы

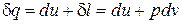. (43)

Выражение удельной потенциальной работы можно представить в виде соотношения

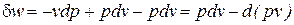, (44)

из которого следует, что

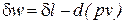; . (45)

После подстановки выражения 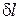(45) в уравнение (43), получим:

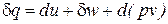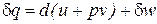, . (46)

Сумма удельной внутренней энергии () и потенциальной
функции (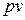) называется удельной энтальпией (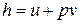) (Дж/кг).

Поскольку энтальпия определяется с помощью параметров состояния (u, р, v), то она является функцией состояния, а для простого тела может быть представлена в функции любых двух параметров, например, р и Т. Дифференциал функции состояния является полным дифференциалом и, следовательно,

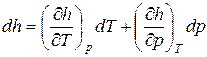. (47)

Подобно полной внутренней энергии энтальпия системы является экстенсивным параметром, зависит от количества вещества и определяется по соотношению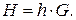

Первое начало термодинамики для 1 кг простого тела по балансу рабочего тела в дифференциальной и интегральной форме можно представить в следующем виде:

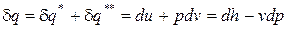; (48)

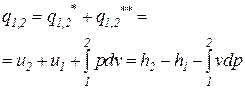. (49)

Математическое выражение первого начала термодинамики по внешнему балансу в дифференциальной и интегральной форме имеет следующий вид:

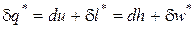; (50)

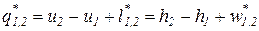. (51)

В реальных процессах эффективная потенциальная (техническая) работа 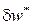равна разности обратимой работы 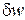и работы необратимых потерь 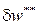, которая превращаются в теплоту внутреннего теплообмена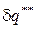

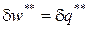. (52)

В обратимых процессах 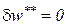и поэтому выражение первого начала термодинамики по внешнему балансу совпадает с выражением первого начала термодинамики по балансу рабочего тела.

Date: 2015-05-09; view: 1608; Нарушение авторских прав