
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение. Полная кинетическая энергия поступательного движения молекул идеального газа определяется выражением:
|
|
Полная кинетическая энергия поступательного движения молекул идеального газа определяется выражением:
Е = N 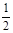 m
m 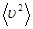 =
= 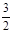 NkT =
NkT = 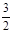 nRT =
nRT = 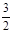 ×3 моля×(8,314 Дж/моль×К)(293 К) = 1,1×104 Дж.
×3 моля×(8,314 Дж/моль×К)(293 К) = 1,1×104 Дж.
7.4. ИЗОПРОЦЕССЫ
Изопроцессом называется процесс, при котором один из параметров состояния (p, V или Т) остается постоянным, а два других изменяются при неизменной массе.
Процесс, происходящий в физической системе при постоянной температуре, называется изотермическим:
Т = const; (7.16)
pV = const. (7.17)
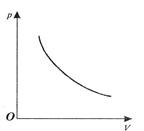
График изотермического процесса в координатах (p, V) представляет собой гиперболу, называемую изотермой (рис. 7.2).
Процесс, происходящий в физической системе при постоянном внешнем давлении, называется изобарным:
p = const; (7.18)
V/Т= const. (7.19)
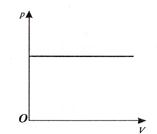
График изобарного процесса в координатах (p, V) или изобара приведен на рис. 7.3.
|
| 
|
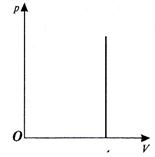
| Рис. 7.2. График изотермического процесса в координатах (р, V) | Рис. 7.3. График изобарного процесса в координатах (р, V) | Рис. 7.4. График изохорного процесса в координатах (р, V) |
Процесс, происходящий в физической системе при постоянном объеме, называется изохорным:
V = const; (7.20)
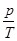 = const. (7.21)
= const. (7.21)
График изохорного процесса в координатах (p, V) или изохора показан на рис. 7.4.
Эти уравнения легко вывести из уравнения Клапейрона-Менделеева (7.1) при Т = const, p = const и V = const соответственно.
7.5. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ
ПО СКОРОСТЯМ
Молекулы идеального газа имеют разные скорости и энергии вследствие хаотического движения. Распределение молекул по скоростям зависеть от температуры газа. Фундаментальное выражение, полученное Максвеллом, описывает распределение молекул по скоростям так:
Nu = 4 pN 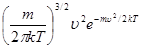 , (7.22)
, (7.22)
где m – масса молекул газа; k – постоянная Больцмана; T – абсолютная температура. Здесь Nu стремится к нулю в случае очень больших и очень малых скоростей.
Типичная кривая распределения приведена на рис. 7.5. Максимум этой кривой соответствует наиболее вероятной скорости:
uнй =  . (7.23)
. (7.23)
Средняя арифметическая скорость молекул определяется выражением:
<u> = 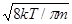 . (7.24)
. (7.24)
Из выражения (7.15) можно получить выражение для средней квадратичной скорости:
<u2> = 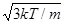 . (7.25)
. (7.25)
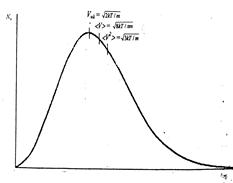
| Рис. 7.5. Распределение молекул NV по скоростям. Здесь: uнй – наиболее вероятная скорость; <u> – средняя арифметическая скорость; <u2> – средняя квадратичная скорость молекул |
Пример
Десять частиц имеют скорости
4, 6, 8, 15, 15, 15, 9, 10, 3, 6 м/с. Определить среднюю арифметическую и наиболее вероятную скорости движения частиц.
Date: 2015-05-09; view: 1087; Нарушение авторских прав