Применение первого начала термодинамики к изопроцессам в идеальном газе

Для равновесных процессов, протекающих в газах, элементарная работа, производимая газом против внешних сил, состоит в работе расширения (2.1), поэтому первое начало термодинамики может быть записано в виде:

dQ=dU+p×dV

Изохорный процесс (V=const). В этом случае, как уже отмечалось, работа, совершаемая газом против внешней силы, равна нулю. Первое начало термодинамики для изохорного процесса примет вид:

dQ=dU (2.7)

Таким образом, в изохорном процессе вся теплота, подведенная к газу, идет на увеличение его внутренней энергии. Используя уравнение (2.5), выразим изменение теплоты dQ через изменение температуры dT

,

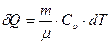где С_u - молярная теплоемкость газа при постоянном объеме. Согласно (2.7) приращение внутренней энергии при этом процессе примет вид:

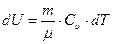, или 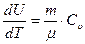. (2.8)

С другой стороны ранее было получено выражение для внутренней энергии идеального газа в зависимости от числа i степеней свободы составляющих его молекул: U=i mRT/(2m). Продифференцировав это соотношение по T, получим формулу:

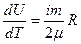, (2.9)

сравнивая которую с (2.8), получим выражение для C_u:

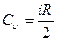(2.10)

Таким образом, молярная теплоемкость при постоянном давлении для идеального газа не зависит от термодинамических параметров, а определяется характером газа (числом степеней свободы молекул).

Изобарный процесс (p=const). Примером изобарного процесса может служить процесс теплообмена с газом, находящимся в цилиндре под поршнем (рис.2.1), нагруженным постоянной внешней силой. В соответствии с (2.2) работа, совершаемая газом против внешней силы, равна:

А_р=р×(V₂-V₁) (2.11)

и может быть найдена как площадь фигуры под линией изобары, которая в координатах (p,V) имеет вид прямоугольника. Уравнение первого начала термодинамики для изобарного процесса имеет вид (2.6), в котором давление следует считать постоянным.

Если обозначить через С_р молярную теплоемкость газа процесса, протекающего при постоянном давлении, то согласно (2.5) выражение для притока тепла при изобарическом нагревании можно записать в виде:

. (2.12)

Приравнивая правые части соотношений (2.6) и (2.12), получим:

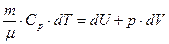
и делением обеих частей равенства на m dT/m преобразуем эту формулу к виду:

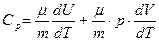. (2.13)

Значение производной dU/dT, входящей в правую часть полученного равенства, можно подставить из формулы (2.9). При вычислении dV/dT можно воспользоваться уравнением состояния pV=m/m RT, но необходимо помнить, что процесс изобарический (p=const). В результате dV/dT=mR/(mp) и выражение (2.13) перейдет в следующее:

С_p=C_u+R (2.14)

Это соотношение называется уравнением Майера. Из него следует, что теплоемкость при изобарическом нагревании всегда больше такого же процесса, происходящего при постоянном объеме (С_р>C_u). Уравнение Майера справедливо в случае идеального газа, но вывод, что (С_р>C_u) имеет место в случае любых газов и многих других систем. Он обязан способности тел расширяться при нагревании. При изохорном нагревании подведенная теплота идет только на увеличение внутренней энергии системы, а при изобарном процессе дополнительно затрачивается на работу, производимую телом при его расширении против сил внешнего давления. Поэтому для нагревания на один градус в изобарическом процессе требуется затратить большее количество тепла, а процесс имеет большую теплоемкость.

Таким образом, молярная теплоемкость C_р идеального газа в процессе изобарического нагревания тоже не зависит от термодинамических параметров:

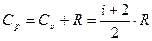(2.15)

и количество теплоты при изобарном нагревании от температуры T₁ до T₂ может быть подсчитано как:

.

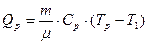Изотермический процесс (T=const). Согласно первому началу термодинамики для любого процесса справедливо:

Q=DU+A

Для идеального газа внутренняя энергия U$ определяется его температурой T, следовательно для изотермического процесса (поскольку DT=0 и DU=0) первое начало дает:

Q_T=A. (2.16)

Таким образом, при изотермическом процессе вся подведенная теплота расходуется на совершение работы газа. При этом подвод тепла не приводит к изменению температуры газа. Теплоемкость газа в таком процессе бесконечна (C_Т= 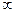). Действительно, какое бы ни было большое количество тепла подведено к газу, изменить его температуру (даже на один градус) не удастся (поскольку T=const).

Найдем работу расширения газа при изотермическом процессе. В соответствии с формулой (2.2)

.

Воспользовавшись уравнением состояния идеального газа найдем закон изменения давления:

,

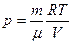который подставим под знак интеграла и вынесем постоянные за знак интегрирования (T=const):

.

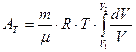После интегрирования будем иметь:

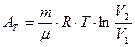, причем Q_T=A_T. (2.17)

Во всех рассмотренных процессах мы рассматривали ситуацию, когда теплота подводится к газу (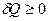). В этом случае газ нагревается (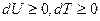), расширяется (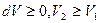) и совершает работу (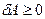). Однако полученные при этом формулы сохраняют свой вид и в обратном процессе сжатия и охлаждения газа. В последнем случае все перечисленные величины имеют ту же абсолютную величину, но обратный знак. Это означает, что для сжатия газа необходимо совершать работу внешними силами (над газом), а тепло газом отдается другим телам.

Date: 2015-05-09; view: 1520; Нарушение авторских прав