Дифференциальное уравнение теплопроводности

Любое физическое явление, можно описать математически, используя аппарат дифференциальных уравнений. Особенно это удобно при исследовании сложных процессов, к которым относится явление теплопроводности. При этом рассматриваются явления, протекающие в бесконечно малых объемах тел при действии бесконечно малых физических величин за бесконечно малые промежутки времени.

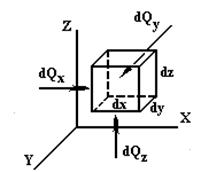
Выделим в теле элементарный параллелепипед (рис. 6.2) с ребрами dx, dy, dz. Температуры граней различны, поэтому через параллелепипед проходит теплота в направлении осей x, y, z.

Через площадку 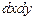за время 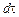, согласно уравнению Фурье проходит теплота

.

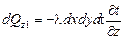Через противоположную грань, расположенную на расстоянии dz от первой отводится теплота

,

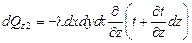где - температура второй грани, а величина 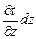определяет изменение температуры в направлении z.

Рис.13.2. К выводу дифференциального уравнения

теплопроводности

Последнее уравнение можно записать в другом виде после раскрытия скобок

.

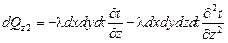Приращение внутренней энергии в параллелепипеде в направлении оси z будет равно разност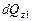и и :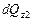

= .

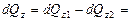
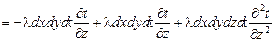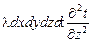Аналогичный вид формул приращения внутренней энергии в параллелепипеде получим для направлений y и x:

, .

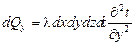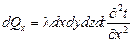Полное приращение внутренней энергии в объеме элементарного параллелепипеда будет равно сумме приращений тепловых потоков в направлении осей x, y, z.

.

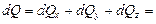
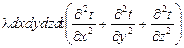С другой стороны, в соответствии с законом сохранения энергии,

,

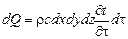где 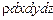- масса параллелепипеда; 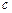- удельная теплоемкость; - изменение температуры за время dt.

Приравнивая левые части полученных уравнений, будем иметь

,

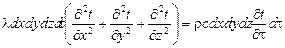откуда получим выражение для изменения температуры

.

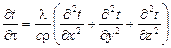Выражение в скобках есть оператор Лапласа, который обычно обозначают сокращенно 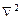(знак 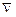читается “набла”); величина 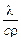называется темпера-туропроводность и обозначается буквой 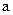. В итоге дифференциальное уравнение теплопроводности принимает вид

.

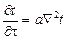Полученное уравнение называется дифференциальным уравнением теплопроводности (или уравнением Фурье) для трехмерного нестационарного температурного поля при отсутствии внутренних источников теплоты. Оно является основным при изучении вопросов нагревания и охлаждения тел в процессе передачи теплоты теплопроводностью, и устанавливает связь между временными и пространственными изменениями температуры в любой точке поля.

Коэффициент температуропроводности 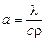является физическим параметром вещества с размерностью 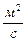. В нестационарных тепловых процессах а характеризует скорость изменения температуры.

Дифференциальное уравнение теплопроводности с источниками теплоты внутри тела имеет вид

,

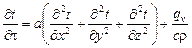где 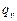- удельное количество выделяемой теплоты в единице объема вещества в единицу времени, .

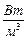Дифференциальное уравнение теплопроводности в цилиндрических координатах с внутренним источником теплоты записывается в виде следующего выражения

,

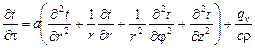где 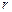- радиус-вектор в цилиндрической системе координат; 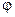- угол.

Date: 2015-05-09; view: 916; Нарушение авторских прав