Частные случаи расположения прямой на плоскости

Рассмотрим общее уравнение прямой на плоскости (9.1):

1). Если 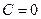, тогда уравнение (9.1) примет вид

.

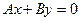Координаты точки 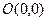удовлетворяют этому уравнению, следовательно, в этом случае прямая проходит через начало координат.

2). Если 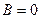, то уравнение (9.1) примет вид

,

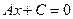или 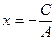, то есть прямая параллельна оси ординат.

3). Если 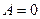, то получим уравнение

,

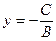в этом случае прямая параллельна оси абсцисс.

4). Если 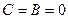, то получим уравнение - это уравнение оси .

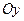5). Если 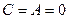, то уравнение 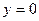определяет ось .

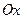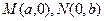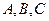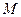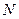6) Пусть прямая не параллельна ни одной оси и даны точки пересечения прямой с осями координат (рис), составим по этим данным уравнение прямой. Воспользуемся общим уравнением прямой на плоскости, в этом уравнении нужно найти коэффициенты , для этого подставим координаты точек и в уравнение, получим: ,

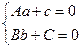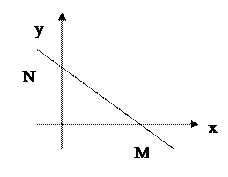
Рис.2.36

следовательно, 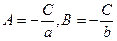, подставляем найденные коэффициенты в (2.41), получаем

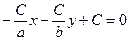или 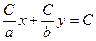, разделим это уравнение на 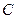, получим уравнение прямой в отрезках:

.

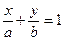Числа 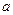и 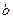показывают, какие отрезки на осях координат отсекает данная прямая.

Пример. Составить уравнение прямой, проходящей через точку 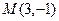и отсекающей на осях координат равные отрезки.

Решение. Так как прямая отсекает на осях координат равные отрезки, то 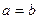, воспользуемся уравнением, подставим координаты точки 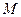в это уравнение, получим

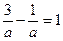, тогда ,

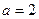подставляем в (2.44), получаем

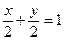или .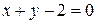

Определение 3. Вектор, параллельный данной прямой или лежащий на этой прямой, называется направляющим вектором прямой.

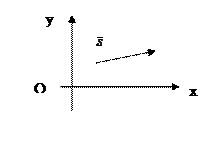
Пусть 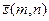- направляющий вектор прямой.

Определение 4. Угловым коэффициентом прямой называется отношение проекции направляющего вектора на ось ординат к его проекции на ось абсцисс.

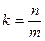
Пусть задан угловой коэффициент прямой 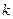и точка пересечения прямой с осью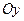 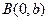. Составим уравнение этой прямой.

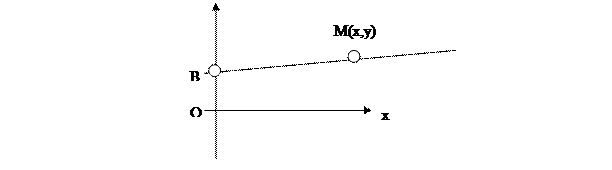
Возьмем произвольную точку 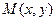на прямой (рис), тогда вектор 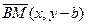будет направляющим, следовательно, 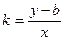, выразив из этого соотношения 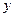, получим уравнение прямой с угловым коэффициентом:

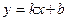. (9.2)

Пусть задана точка 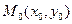через которую проходит прямая и угловой коэффициент этой прямой 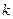. Надо составить уравнение этой прямой. Для этого воспользуемся уравнением (9.2), в котором требуется найти коэффициент 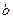. Подставим в уравнение (9.2) координаты точки 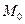, получим 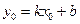, вычитая из (9.2) данное равенство, получим:

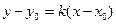. (9.3)

Это уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом. Если в уравнении (9.3) угловой коэффициент 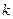будет принимать всевозможные значения, то это уравнение будет определять пучок прямых с центром в точке .

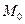Пусть задана точка 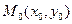, через которую проходит прямая, и направляющий вектор 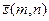этой прямой. Составим уравнение этой прямой, воспользовавшись уравнением (9.3):

,

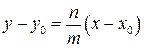преобразовав это равенство, получим каноническое уравнение прямой:

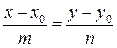. (9.4)

Уравнение (9.4) можно рассматривать как пропорцию, поэтому

,

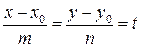отсюда получаем параметрические уравнения прямой на плоскости:

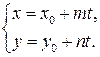(9.5)

Пусть даны две точки 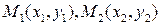, через которые проходит прямая. Составим уравнение данное прямой. Воспользуемся каноническим уравнением прямой (9.4), где в качестве направляющего вектора возьмем вектор :

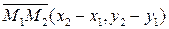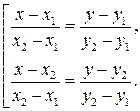(9.6)

Оба уравнения в (9.6) являются уравнениями прямой, проходящей через две заданные точки.

Date: 2015-05-09; view: 1099; Нарушение авторских прав