Капиллярные явления. Формула Лапласса

Если поместить узкую трубку (капилляр) одним концом в жидкость, налитую в ши­рокий сосуд, то вследствие смачивания или несмачивания жидкостью стенок ка­пилляра кривизна поверхности жидкости в капилляре становится значительной. Ес­ли жидкость смачивает материал трубки, то внутри ее поверхность жидкости — ме­ниск — имеет вогнутую форму, если не смачивает — выпуклую (рис. 101).

Под вогнутой поверхностью жидкости появится отрицательное избыточное дав­ление, определяемое по формуле (68.2). Наличие этого давления приводит к тому, что жидкость в капилляре поднимается, так как под плоской поверхностью жидко­сти в широком сосуде избыточного давле­ния нет. Если же жидкость не смачивает стенки капилляра, то положительное из­быточное давление приведет к опусканию жидкости в капилляре. Явление изменения высоты уровня жидкости в капиллярах называется капиллярностью. Жидкость в капилляре поднимается или опускается на такую высоту h, при которой давление столба жидкости (гидростатическое дав­ление) r gh уравновешивается избыточным давлением Dр, т. е.

2s/R=rgh,

где r — плотность жидкости, g — ускоре­ние свободного падения.

Если m — радиус капилляра, q — крае­вой угол, то из рис. 101 следует, что (2scosq)/r= rgh, откуда

h=(2scosq)/(rgr). (69.1)

В соответствии с тем, что смачиваю­щая жидкость по капилляру поднимается, а несмачивающая — опускается, из фор-мулы (69.1) при q<p/2 (cosq>0) полу­чим положительные значения Л, а при 0>p/2 (cosq<0) —отрицательные. Из выражения (69.1) видно также, что высо­та поднятия (опускания) жидкости в ка­пилляре обратно пропорциональна его ра­диусу. В тонких капиллярах жидкость под­нимается достаточно высоко. Так, при полном смачивании (6 = 0) вода (r=1000 кг/м³, s=0,073 Н/м) в капилляре диаметром 10 мкм поднимается на высоту h»3 м.

Капиллярные явления играют боль­шую роль в природе и технике. Например, влагообмен в почве и в растениях осуще­ствляется за счет поднятия воды по тон­чайшим капиллярам. На капиллярности основано действие фитилей, впитывание влаги бетоном и т. д.

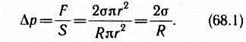
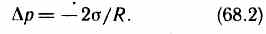
Следовательно, давление внутри жидкости под вогнутой поверхностью меньше, чем в газе, на величину D р.

Формулы (68.1) и (68.2) являются частным случаем формулы Лапласа, оп­ределяющей избыточное давление для произвольной поверхности жидкости двоя­кой кривизны:

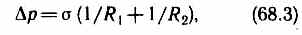
где R ₁ и R ₂ — радиусы кривизны двух любых взаимно перпендикулярных нор­мальных сечений поверхности жидкости в данной точке. Радиус кривизны положи­телен, если центр кривизны соответствую­щего сечения находится внутри жидкости, и отрицателен, если центр кривизны на­ходится вне жидкости.

Для сферической искривленной повер­хности (R ₁ =R ₂ =R) выражение (68.3) пе­реходит в (68.1), для цилиндрической (R ₁ =R и R ₂=¥) — избыточное давление

Dр=s(1/R+1/¥)=s/ R.

Для плоской поверхности (R ₁= R ₂=¥) силы поверхностного натяжения избыточ­ного давления не создают.

Date: 2015-05-09; view: 984; Нарушение авторских прав