Принцип Ле Шателье-Брауна. Примеры проявления принципа Ле Шателье-Брауна

Устойчивость состояния обеспечивается тем, что при выводе системы из состояния равновесия в ней возникают факторы, стремящиеся вернуть ее в состояние ТД равновесия. Это положение было установлено Ле Шателье и обосновано Брауном и носит название принцип Ле Шателье-Брауна. Принцип позволяет предсказать направление, в котором под влиянием внешнего воздействия изменится ТД процесс, протекающий в произвольной системе.

Принцип Ле Шателье-Брауна: если на систему, находящуюся в устойчивом ТД равновесии, воздействуют внешние факторы, стремящиеся вывести ее из этого состояния, то в системе возникают процессы, стремящиеся уничтожить изменения, вызываемые внешними воздействиями.

Математически принцип выражается неравенством 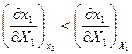, где в системе сохраняется химический состав и масса, 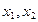- параметры, определяющие состояние системы, 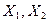- обобщенные силы, соответствующие этим параметрам. Если в системе, в которой поддерживаются постоянными параметры 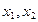, мы начинаем внешним воздействием 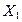изменять параметр 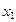, то это вызовет изменение 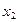и 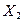, а мерой воздействия является величина 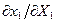. Но при внезапном увеличении 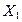происходящий процесс вначале можно рассматривать как при постоянном 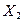, следовательно, в это время приложенное воздействие характеризуется производной 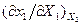. Когда же снова наступит равновесие и параметр 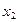примет поддерживаемое внешней средой прежнее значение, то изменение величины 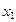за счет внешнего воздействия будет определяться производной 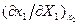. Принцип утверждает, что в новом равновесном состоянии, в которое переходит система, изменение параметра 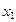ослаблено за счет внешнего воздействия.

Примеры проявления принципа Ле Шателье-Брауна:

1. Увеличим внешнее давление на тело, уменьшая его объем. При этом возникает изменение температуры, которое направлено так, что стремится снова увеличить объем; поэтому те тела, которые от нагревания сжимаются (например, вода при 4°С), будут от сжатия охлаждаться.

2. Сообщим смеси из льда и воды некоторое количество теплоты. Тогда лед начинает таять, благодаря чему не происходит повышение его температуры, которое иначе имело бы место.

3. Если имеются два вещества в состоянии химического равновесия и им сообщили некоторое количество теплоты, то произойдет та реакция, которая охлаждает систему. Следовательно, при повышении температуры будут разлагаться вещества, возникающие путем экзотермической реакции, и, наоборот, будут возникать эндотермические соединения.

4. Для соли, находящейся в насыщенном растворе, повышение температуры вызывает растворе, если последнее связано с охлаждением; в противном случае происходит выпадение кристаллов.

5. Если электрический ток проходит через спай двух металлов, то температура спая изменяется в таком направлении, что возникающей термоэлектрический ток стремится ослабить ток, пропускаемый через спай (явление Пельтье).

Из примеров видно, что принцип Ле Шателье-Брауна обусловлен устойчивостью состояния. Если бы первичный процесс усиливался еще дальше благодаря вызванному им вторичному процессу, то это привело бы к полному расстройству равновесия в системе.

55.Начала статистической физики: исходные понятия теории вероятности.

Как мы раньше говорили, с одной стороны, информация о положениях и скоростях всех отдельных частиц системы идеального газа является наиболее полной мыслимой информацией, а с другой стороны, в своей непосредственной форме она неприменима для анализа свойств и поведения системы. Чтобы информацию, содержащуюся в этих сведениях, можно было использовать, необходимо свести ее к некоторым обобщенным характеристикам совокупности частиц таким образом, чтобы они отражали наиболее существенные свойства этой совокупности, были бы легко обозримыми и сформулированными математически. Эти вопросы разработаны в теории вероятностей и математической статистике.

Разделим объем, который занят идеальным газом, на две равные части. Будем считать, что можем различать частицы и следить за положением отдельной частицы, не оказывая актом наблюдения существенного влияния на ее движение и состояние наблюдаемой системы в целом. Допустим, что система находится в неизменных внешних условиях. Рассмотрим событие, состоящее в том, что изучаемая частица находится в одной из половин объема. Тогда результат каждого наблюдения сводится к утверждению, что событие либо произошло, т.е. частица находится в данной половине объема, либо не произошло, т.е. ее нет в этой половине. Обозначим 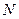- общее число наблюдений или «испытаний»; 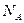- число испытаний, когда событие произошло, т.е. частица находилась в рассматриваемой половине объема; 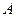- само событие. Вероятность наступления события 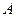определяется формулой:

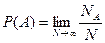
Здесь существенно очень большое 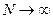число испытаний в системе, находящейся в неизменных условиях. Вместо требований испытаний над одной и той же системой в неизменных условиях можно говорить о совокупности отдельных испытаний над большим числом одинаковых систем. Это большое число одинаковых систем называется ансамблем систем.

Для непрерывных случайных величин вводится понятие плотности вероятности. Плотностью вероятности равняется вероятность нахождения молекулы в бесконечно малом объеме, отнесенном к этому объему:

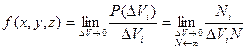, где 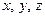- координаты точки, к которой стягивается бесконечно малый объем .

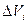Из этого определения следует, что если произвести 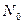наблюдений, то в объеме 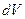в окрестности точки 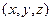молекула будет обнаружена в 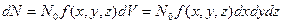случаях.

В конечном объеме 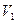молекула окажется обнаруженной 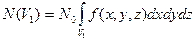раз. Отсюда следует, что вероятность 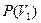быть обнаруженной при наблюдении в объеме 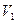для молекулы равна: .

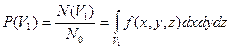Если в качестве объема взять все пространство 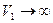, то при каждом испытании частица окажется в какой-то точке пространства и, следовательно, число наблюдений частицы в объеме 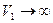равно числу испытаний 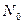, т.е. 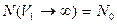и следовательно вероятность нахождения частицы в объеме равна единице. Условие

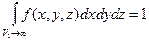
называется условием нормировки плотности вероятности. Оно выражает факт существования молекулы.

Среднее значение непрерывно изменяющейся величины (еще называют математическим ожиданием случайной величины с учетом вероятности):

,

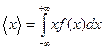где - плотность вероятности распределения случайной величины х.

Дисперсия. «Разброс» величины около ее среднего значения характеризуется дисперсией. Она определяется средним квадратом отклонения рассматриваемой величины от ее среднего значения и задается формулой для непрерывной случайной величины:

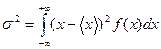
Корень квадратный из дисперсии называется стандартным или среднеквадратичным отклонением.

Функция распределения вероятностей. Вероятность того, что случайная величина х принимает значения, меньшие некоторого заданного числа х₀, т.е. 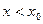определяется формулой:

.

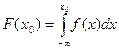Функция называется функцией распределения вероятностей.

В физике принято характеризовать распределение вероятностей посредством плотности вероятности. При этом слова «плотность» и «вероятность» опускаются, и говорится просто о распределении. Например, функция 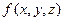называется просто функцией распределения координат. Можно говорить о функциях распределения скоростей, импульсов и т.д. вид функции распределения зависит от физических условий, свойств частиц и т.д. Однако имеются наиболее типичные распределения, которые реализуются при весьма общих физических условиях. Это распределение Гаусса, Биномиальное распределение, распределение Пуассона и т.д.

56.Начала статистической физики: макро- и микросостояния, статистический ансамбль, микроканонический ансамбль, постулат равновероятности.

Состояние газа, характеризуемое его давлением, температурой и объемом, называется макроскопическим.

Состояние газа, характеризуемое положениями и скоростями всех его частиц, называется микроскопическим. Если число частиц n (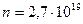 в 1см³ при н.у.) то микроскопическое состояние газа характеризуется 6 п числами (микропараметрами): 3 п координатами 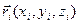всех частиц и 3 п проекциями их скоростей . Все эти числа следует рассматривать как случайные величины.

В равновесном состоянии Р,V, Т – фиксированные величины, а вот 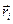и 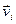могут меняться. Возьмем очень большое число 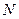совершенно одинаковых сосудов, каждый из которых имеет объем 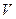. В каждом из сосудов находится одинаковое число n одинаковых частиц.

Сосуд с заключенными в нем частицами называется статистической системой.

Совокупность одинаковых статистических систем называется статистическим ансамблем.

Микроканонический ансамбль состоит из одинаковых изолированных систем с одинаковой энергией. Кроме микроканонических ансамблей в статистической физике рассматриваются также канонические и некоторые другие ансамбли.

Ø Допустим частицы, входящие в систему микроканонического ансамбля, считаются пронумерованными, пронумерованы также и ячейки, в которых могут находиться частицы.

Ø Известно, что атомы и молекулы имеют определенные размеры. Их диаметр имеет порядок 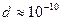м. Каждая молекула или атом занимает объем порядка 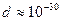м³, таким образом, в 1 м³ имеется всего 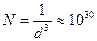ячеек. С другой стороны в 1 м³ воздуха при нормальных условиях находится 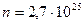частиц. Это означает, что в типичных условиях одна частица приходится на 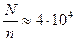ячеек.

Ø В некоторый момент времени некоторая частица находится в различных системах ансамбля в различных ячейках. Если ансамбль содержит очень большое число систем 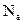, то число систем, в которых рассматриваемая частица окажется в ячейке 1, равна числу систем, в которых она оказалась в ячейке 2. Для данной частицы все возможные положения равновероятны. Микросостояние характеризуется положением всех частиц, входящих в систему, т.е. конкретным распределением этих частиц по ячейкам, на которые разбит объем.

Ø Поскольку все ячейки для каждой из частиц равновозможны, логично заключить, что все распределения частиц по ячейкам также равновозможны. А это означает, что все микросостояния равновероятны.

Одно и тоже макроскопическое состояние осуществляется в большом числе систем ансамбля, находящихся в различных микроскопических состояниях. Следовательно, данное макросостояние характеризуется большим числом микросостояний.

В основе всей статистической физики лежат не доказанные в общем случае постулат равновероятности и эргодическая гипотеза. В состоянии ТД равновесия все микросостояния равновероятны. Это постулат равновероятности.

57.Начала статистической физики: эргодическая гипотеза, статистический вес, статистическое толкование энтропии.

Пусть наша система состоит из одной частицы. Мы следим за скоростью частицы. Естественно нас интересует средняя скорость частицы:

.

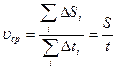Эргодическая гипотеза утверждает, что такая средняя скорость равняется средней скорости, вычисленной по ансамблю систем, т.е. среднее значение величины, вычисленное по времени равняется среднему значению величины, вычисленному по ансамблю систем. Пусть число систем в ансамбле 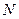, в некоторый момент времени :

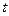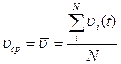
Впервые эта гипотеза была высказана в 1871 г. Л. Больцманом (1844-1906). Затем Дж. Максвелл в 1879 г. проанализировал возможность замены средних значений по времени средними значениями по ансамблю. Используя эту гипотезу, мы можем вопрос об изучении параметров системы, меняющихся со временем, свести к одномоментному усреднению по ансамблю!

Статистический вес Г: определяется числом микросостояний, реализующих данное макросостояние. Причем справедлив постулат равновероятности всех микросостояний.

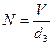Общее число микросостояний равно, очевидно, числу способов, которыми можно разместить частиц по ячейкам, где 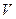- объем занимаемый системой из частиц. Конкретную формулу дает комбинаторика. Отметим, что статистический вес для моля кислорода при нормальном атмосферном давлении и комнатной температуре 20°С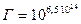

Статистический вес Г еще называют термодинамической вероятностью состояния системы. Т.к. это число способов, которыми может быть реализовано данное макросостояние системы, по определению, . Таким образом, термодинамическая вероятность не есть вероятность в математическом смысле (т.к. ).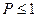

Будем отличать макросостояния номерами 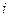, 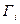- статистический вес 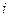-го макросостояния.

Используя это понятие, Больцман в 1872 г. Предложил статистическое толкование энтропии. Это более глубокое толкование.

Согласно Больцману, энтропия системы и статистический вес Г связаны между собой соотношением

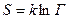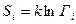или и

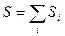- если система состоит из подсистем с .

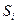Она определяется логарифмом числа микросостояний, с помощью которых было реализовано данное макросостояние.

Тогда статистический вес системы выражается через произведение 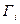подсистем.

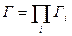
Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы.

Формула Больцмана позволяет дать энтропии следующее определение (статистическое толкование).

Энтропия является мерой неупорядоченности системы. Энтропия есть количественная мера беспорядка системы многих частиц.

В самом деле, чем больше число микросостояний реализующих данное макросостояние, тем больше энтропия.

В изолированной ТД системе все процессы идут в направлении возрастания энтропии, в направлении наиболее вероятного макросостояния (равновесного). Энтропия возрастает по II началу ТД, следовательно, естественные процессы стремятся перевести систему в состояние с наибольшим беспорядком. Это тенденция, хотя возможны отдельные флуктуации, понижающие энтропию.

58.Начала статистической физики: флуктуации.

Ø Говорят, что величина флуктуирует, если ее значение колеблется около среднего. В статистической физике и термодинамике обычно имеются в виду флуктуации внутренних параметров в состоянии термодинамического равновесия.

Мерой флуктуаций является стандартное отклонение от среднего значения, которое определено равенством для дискретных величин:

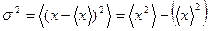
При вычислении этой величины усреднение по времени можно заменить усреднением по ансамблю.

Стандартное отклонение растет медленнее, чем общее число частиц в системе, в то время как среднее растет пропорционально числу частиц в системе. Следовательно, относительное стандартное отклонение убывает сростом числа частиц в системе.

Расчет относительной величины флуктуации с помощью распределения Пуассона дает величину:

.

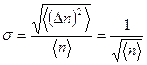Отметим, что относительная роль флуктуаций возрастает с уменьшением области, в которой эти флуктуации рассматриваются. Если область стремится к величине объема системы, то число частиц в этой области стремится к числу частиц системы.

Так как флуктуации уменьшаются как 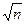, следовательно, с ростом числа частиц в макросистемах флуктуации становятся ничтожно малыми.

Поэтому поведение системы большого числа частиц можно описывать с помощью средних величин, характеризующих систему.

С 59 ПО 63 НЕ РАЗДЕЛИЛА ИЛИ НЕ НАШЛА!

59.Классическая статистика Максвелла-Больцмана: подсчет числа состояний.

60.Классическая статистика Максвелла-Больцмана: вывод функции распределения Больцмана (дискретное распределение).

Date: 2015-05-09; view: 4971; Нарушение авторских прав