
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод ТД потенциалов
|
|
Метод термодинамических потенциалов или метод характеристических функций был развит Гиббсом. Это аналитический метод, базирующейся на использовании основного уравнения термодинамики для квазистатических процессов 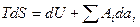 .
.
Идея метода состоит в том, что основное уравнение термодинамики позволяет для системы в различных условиях ввести некоторые функции состояния, называемые термодинамическими потенциалами, изменение которых при изменении состояния является полным дифференциалом; пользуясь этим можно составить уравнения, необходимые для анализа того или иного явления.
С 41 ПО 46 НЕ РАЗДЕЛИЛА!СМОТРЕТЬ ТУТ(то что красным)!!!:
Метод термодинамических потенциалов или метод характеристических функций был развит Гиббсом. Это аналитический метод, базирующейся на использовании основного уравнения термодинамики для квазистатических процессов 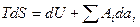 .
.
Идея метода состоит в том, что основное уравнение термодинамики позволяет для системы в различных условиях ввести некоторые функции состояния, называемые термодинамическими потенциалами, изменение которых при изменении состояния является полным дифференциалом; пользуясь этим можно составить уравнения, необходимые для анализа того или иного явления.
Рассмотрим простые системы. В этом случае для квазистатических процессов основное уравнение ТД имеет вид 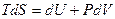 для закрытой системы.
для закрытой системы.
Как изменится это уравнение, если будет меняться число частиц? Внутренняя энергия и энтропия пропорциональны числу частиц в системе: 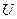 ~
~ 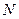 ,
, 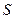 ~
~ 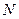 , следовательно
, следовательно 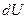 ~
~ 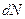 ,
, 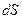 ~
~ 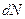 и уравнение будет иметь вид
и уравнение будет иметь вид 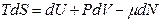 для открытой системы, где
для открытой системы, где
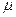 - химический потенциал будет обобщенной силой для независимой переменной
- химический потенциал будет обобщенной силой для независимой переменной 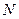 числа частиц в системе.
числа частиц в системе.
Это уравнение связывает пять величин, две из которых являются функциями состояния: 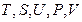 . Само же состояние простой системы определяется двумя параметрами. Поэтому, выбирая из пяти названных величин две в качестве независимых переменных, мы получаем, что основное уравнение содержит еще три неизвестные функции. Для их определения необходимо к основному уравнению добавить еще два уравнения, которыми могут быть термическое и калорическое уравнения состояния:
. Само же состояние простой системы определяется двумя параметрами. Поэтому, выбирая из пяти названных величин две в качестве независимых переменных, мы получаем, что основное уравнение содержит еще три неизвестные функции. Для их определения необходимо к основному уравнению добавить еще два уравнения, которыми могут быть термическое и калорическое уравнения состояния: 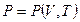 ,
, 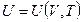 , если в качестве независимых параметров выбраны
, если в качестве независимых параметров выбраны 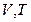 .
.
Однако определение этих трех неизвестных величин упрощается с введением термодинамических потенциалов.
Выразим из основного уравнения 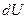 :
: 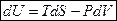 для закрытой системы
для закрытой системы
или для открытой системы 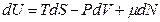
Мы видим, что приращение внутренней энергии полностью определяется приращением энтропии и приращением объема, т.о. если мы в качестве независимых переменных выберем 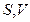 или
или 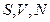 для открытой системы, то для определения других трех переменных нам нужно знать лишь одно уравнение
для открытой системы, то для определения других трех переменных нам нужно знать лишь одно уравнение 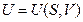 для внутренней энергии как функции
для внутренней энергии как функции 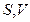 или
или 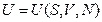 как функции
как функции 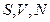 .
.
Так, зная зависимость 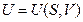 , можно с помощью основного ТД тождества простым дифференцированием (взяв первые производные) определить обе другие термические переменные:
, можно с помощью основного ТД тождества простым дифференцированием (взяв первые производные) определить обе другие термические переменные:
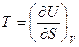 или
или 
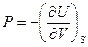 или
или 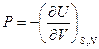 и
и 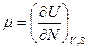 .
.
Если взять вторые производные от 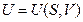 , то можно определить калорические свойства системы:
, то можно определить калорические свойства системы: 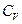 и
и  - адиабатический модуль упругости системы (
- адиабатический модуль упругости системы (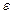 определяет изменение давления \ упругости \ на единицу изменения объема и представляет собой обратную величину коэффициента сжимаемости):
определяет изменение давления \ упругости \ на единицу изменения объема и представляет собой обратную величину коэффициента сжимаемости):
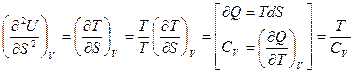 , откуда
, откуда
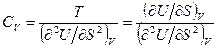 .
.
 , откуда
, откуда 
Учитывая, что 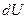 - полный дифференциал, и приравнивая смешанные производные
- полный дифференциал, и приравнивая смешанные производные 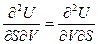 , находим соотношение между двумя свойствами системы – изменение температуры при ее адиабатическом расширении и изменение давления при изохорическом сообщении теплоты системе:
, находим соотношение между двумя свойствами системы – изменение температуры при ее адиабатическом расширении и изменение давления при изохорическом сообщении теплоты системе:
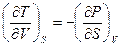 .
.
Таким образом, внутренняя энергия 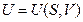 как функция переменных
как функция переменных 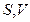 , является характеристической функцией. Ее первые производные определяют термические свойства системы, вторые – калорические свойства системы, смешанные - соотношения между другими свойствами системы. Установление таких связей и составляет содержание метода ТД потенциалов. А
, является характеристической функцией. Ее первые производные определяют термические свойства системы, вторые – калорические свойства системы, смешанные - соотношения между другими свойствами системы. Установление таких связей и составляет содержание метода ТД потенциалов. А 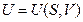 является одним из множества ТД потенциалов.
является одним из множества ТД потенциалов.
Мы можем найти выражение для ТД потенциалов, его явный, только для 2-х систем, одной из которых является идеальный газ, другой равновесное излучение, т.к. для них известны и уравнения состояния и внутренняя энергия как функция параметров. Для всех других систем ТД потенциалы находятся или из опыта, или методами статистической физики, и потом с помощью полученных ТД соотношений определяют уравнения состояния и другие свойства. Для газов ТД функции чаще всего вычисляются методами статистической физики, для жидкостей и твердых тел они обычно находятся экспериментально с помощью калорических определений теплоемкости.
Получим выражение для внутренней энергии идеального газа, как ТД потенциала, т.е. как функции 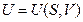 :
:
Для идеального газа  , внутренняя энергия зависит только от
, внутренняя энергия зависит только от 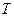 ,
,
с другой стороны энтропия идеального газа зависит от 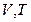 :
: 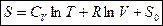 . Выразим из второго уравнения
. Выразим из второго уравнения 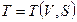 и подставим в первое уравнение:
и подставим в первое уравнение:
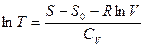 , прологарифмируем
, прологарифмируем
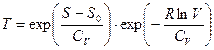 , учтем, что
, учтем, что 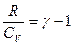
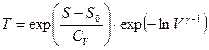 , преобразуя второй множитель, получим:
, преобразуя второй множитель, получим:
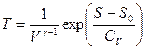 . Подставим полученное выражение в первое уравнение и получим ТД потенциал внутренняя энергия:
. Подставим полученное выражение в первое уравнение и получим ТД потенциал внутренняя энергия: 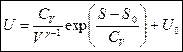 .
.
Внутренняя энергия в качестве ТД потенциала с практической точки зрения неудобна тем, что одна из ее независимых переменных энтропия 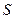 непосредственно, подобно величинам
непосредственно, подобно величинам 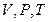 , не может быть измерена.
, не может быть измерена.
Рассмотрим другие ТД потенциалы, преобразуем основное термодинамическое тождество, так чтобы в него входили дифференциалы 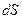 и
и 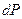 .
.
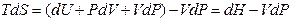 Þ
Þ 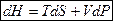
Мы видим, что ТД функция энтальпия 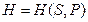 является ТД потенциалом при независимых переменных
является ТД потенциалом при независимых переменных 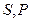 , поскольку производные от этой функции даю остальные характеристики системы.
, поскольку производные от этой функции даю остальные характеристики системы.
Термические 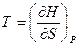 ,
, 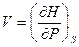 дают первые производные.
дают первые производные.
Калорические 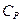 и адиабатический модуль упругости
и адиабатический модуль упругости  ;
;
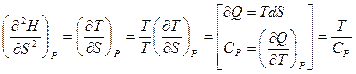 , или
, или
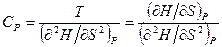 .
.
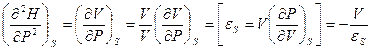 , или
, или
 дают вторые производные.
дают вторые производные.
Связь двух свойств системы, а именно, адиабатического изменения температуры при изменении давления и изобарического изменения объема при сообщении системе теплоты получим, рассчитав смешанные производные:
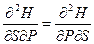 дают
дают 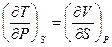 .
.
Рассмотрим ТД потенциал, в независимых переменных, удобных для измерения. Преобразуем основное ТД тождество, так чтобы в него входили дифференциалы 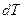 и
и 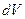 .
.
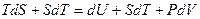 Þ
Þ 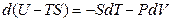 Þ
Þ 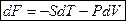
Мы видим, что ТД функция 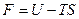 свободная энергия или функция Гельмгольца
свободная энергия или функция Гельмгольца 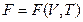 является ТД потенциалом при независимых переменных
является ТД потенциалом при независимых переменных 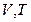 , поскольку производные от этой функции даю остальные характеристики системы.
, поскольку производные от этой функции даю остальные характеристики системы.
Термические 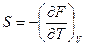 ,
, 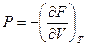 дают первые производные.
дают первые производные.
Калорические теплоемкость 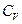 и коэффициент сжимаемости
и коэффициент сжимаемости 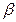 - вторые производные:
- вторые производные:
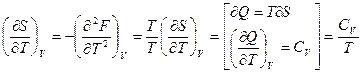 , отсюда следует
, отсюда следует 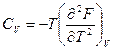 ;
;
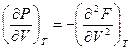 , отсюда следует
, отсюда следует 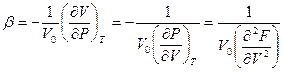 .
.
Смешанные производные устанавливают связь между двумя свойствами системы – изменением энтропии при ее изотермическом расширении и изменением давления при изохорическом нагревании:
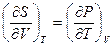 .
.
Рассмотрим еще одну функцию, с другим набором переменных, удобных для измерения. Преобразуем основное ТД тождество, так чтобы в него входили дифференциалы 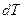 и
и 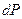 .
. 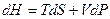
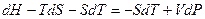 Þ
Þ 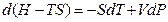 Þ
Þ 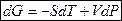
ТД функция 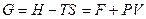 называется потенциалом Гиббса, свободная энергия Гиббса
называется потенциалом Гиббса, свободная энергия Гиббса 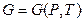 является ТД потенциалом при независимых переменных
является ТД потенциалом при независимых переменных 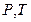 , поскольку производные от этой функции даю остальные характеристики системы.
, поскольку производные от этой функции даю остальные характеристики системы.
Термические 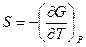 ,
, 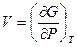 , позволяющие зная явный вид функции
, позволяющие зная явный вид функции 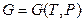 найти термическое уравнение состояния
найти термическое уравнение состояния 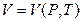 системы.
системы.
Калорические теплоемкость 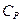 и коэффициент сжимаемости
и коэффициент сжимаемости 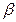 :
:
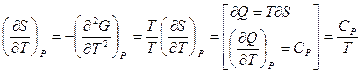 , отсюда следует
, отсюда следует 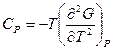 ;
;
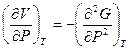 , отсюда следует
, отсюда следует 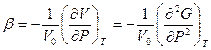 .
.
Смешанные производные устанавливают связь между двумя свойствами системы –
изменением энтропии при ее изотермическом изменении давления и изменением объема при изобарическом нагревании:
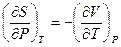 .
.
Как видим, в общем случае, термодинамические потенциалы 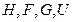 есть функции трех переменных для открытых однокомпонентных систем
есть функции трех переменных для открытых однокомпонентных систем 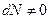 и функциями всего двух переменных для закрытых систем
и функциями всего двух переменных для закрытых систем 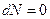 . Каждый ТД потенциал содержит в себе полностью все характеристики системы.
. Каждый ТД потенциал содержит в себе полностью все характеристики системы.
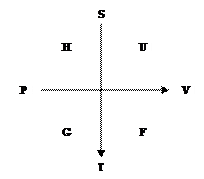 Существует мнемонический метод запоминания ТД потенциалов, их переменных и запись полных дифференциалов.
Существует мнемонический метод запоминания ТД потенциалов, их переменных и запись полных дифференциалов.
На осях 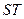 и
и 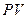 стрелки показывают знаки, если пару переменных брать против направления стрелки, то со знаком (-), Если по направлению стрелки, то со знаком (+).
стрелки показывают знаки, если пару переменных брать против направления стрелки, то со знаком (-), Если по направлению стрелки, то со знаком (+).
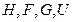 являются ТД потенциалами, если выражены, как функции переменных стоящих справа и слева, например:
являются ТД потенциалами, если выражены, как функции переменных стоящих справа и слева, например:
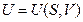 ,
, 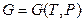 ,
, 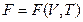 ,
, 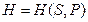 .
.
В принципе можно брать любую функцию, и она будет являться ТД потенциалом от рядом стоящих переменных. ТД потенциал является полным дифференциалом от своих переменных, например:
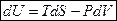 ,
, 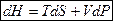 ,
, 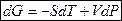 ,
, 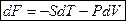
в записи мы учли знаки перед обобщенными силами.
Эта схема позволяет записать функции состояния, как функцию все пяти переменных:
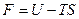 - линия, соединяющая
- линия, соединяющая 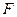 и
и 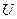 , параллельна и направлена против оси
, параллельна и направлена против оси 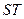 ;
;
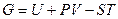 - проекция линии, соединяющей
- проекция линии, соединяющей 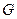 и
и 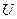 , положительна на ось
, положительна на ось 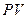 и отрицательна на ось
и отрицательна на ось 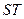 ;
;
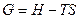 - линия, соединяющая
- линия, соединяющая 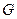 и
и 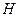 , параллельна и направлена против оси
, параллельна и направлена против оси 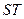 ;
;
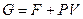 - линия, соединяющая
- линия, соединяющая 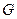 и
и 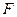 , параллельна и направлена вдоль оси
, параллельна и направлена вдоль оси 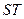 ; т.д.
; т.д.
Различные ТД потенциалы связаны между собой так, что если известны одни из них, то можно найти другие. При этом внутренняя энергия 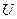 связана со свободной энергией
связана со свободной энергией 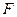 таким же дифференциальным уравнением, как энтальпия
таким же дифференциальным уравнением, как энтальпия 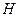 с ТД потенциалом Гиббса. Действительно, из
с ТД потенциалом Гиббса. Действительно, из 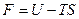 и выражения
и выражения 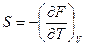 получаем уравнение Гиббса-Гельмгольца
получаем уравнение Гиббса-Гельмгольца 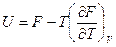 для
для 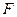 ; из
; из 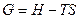 и выражения
и выражения 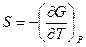 получим
получим 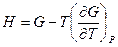 для
для 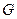 .
.
Метод ТД потенциалов и метод циклов – два метода применяемых в ТД для исследования физических явлений.
Date: 2015-05-09; view: 1366; Нарушение авторских прав