
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

III начало ТД. Следствия III начала ТД
|
|
III начало ТД: по мере приближения температуры к абсолютному нулю энтропия всякой равновесной системы при изотермических процессах перестает зависеть от каких-либо термодинамических параметров состояния и в пределе 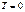 принимает одну и туже для всех систем постоянную величину, которую можно положить равной нулю.
принимает одну и туже для всех систем постоянную величину, которую можно положить равной нулю.
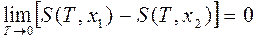 или
или 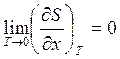 ,где
,где 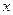 - любой термодинамический параметр.
- любой термодинамический параметр.
Постоянство энтропии 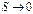 при
при 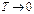 согласно III начала ТД означает что изотермический процесс является одновременно и изоэнтропическим, а следовательно, и адиабатическим. Таким образом, по третьему началу ТД нулевая изотерма совпадает с нулевой адиабатой.
согласно III начала ТД означает что изотермический процесс является одновременно и изоэнтропическим, а следовательно, и адиабатическим. Таким образом, по третьему началу ТД нулевая изотерма совпадает с нулевой адиабатой.
Некоторые следствия III начала ТД:
1) Недостижимость абсолютного нуля температуры.
Из третьего начала ТД непосредственно следует недостижимость абсолютного нуля температуры. Действительно, нулевая изотерма 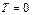 совпадает с нулевой изоэнтропой
совпадает с нулевой изоэнтропой 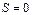 , т.е. с граничным членом семейства
, т.е. с граничным членом семейства 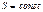 . Но охлаждение осуществляется в результате адиабатического процесса, когда система производит работу за счет убыли своей внутренней энергии. Так как адиабаты
. Но охлаждение осуществляется в результате адиабатического процесса, когда система производит работу за счет убыли своей внутренней энергии. Так как адиабаты 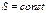 не пересекаются, то состояние с
не пересекаются, то состояние с 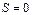 не может быть достигнуто никаким адиабатическим процессом, поэтому нельзя достигнуть ни в каком конечном процессе и абсолютный нуль температуры, совпадающей с
не может быть достигнуто никаким адиабатическим процессом, поэтому нельзя достигнуть ни в каком конечном процессе и абсолютный нуль температуры, совпадающей с 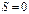 ; к нему можно лишь асимптотически приближаться.
; к нему можно лишь асимптотически приближаться.
2) Термические коэффициенты обращаются в ноль при 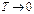 .
.
Термический коэффициент расширения 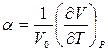 и термический коэффициент давления
и термический коэффициент давления 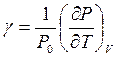 , как и вообще термодинамические величины
, как и вообще термодинамические величины 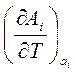 и
и 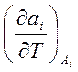 , характеризующие поведение системы при изменении температуры, могут быть получены дифференцированием соответствующих обобщенных сил
, характеризующие поведение системы при изменении температуры, могут быть получены дифференцированием соответствующих обобщенных сил 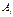 по температуре, где
по температуре, где 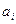 - соответствующий данной обобщенной силе независимый параметр.
- соответствующий данной обобщенной силе независимый параметр.
Используя первое начало ТД, нетрудно убедится, что 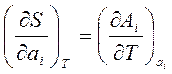 , а так как энтропия перестает зависеть от параметров состояния, то, следовательно, и термические коэффициенты обращаются в ноль.
, а так как энтропия перестает зависеть от параметров состояния, то, следовательно, и термические коэффициенты обращаются в ноль.
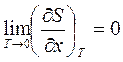 Þ
Þ 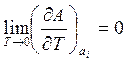 .
.
В частном случае если в качестве обобщенной силы 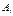 выбираем
выбираем 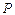 и соответственно,
и соответственно, 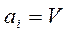 , то
, то 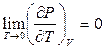 Þ
Þ 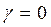 при
при 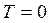 . Принимая в качестве обобщенных сил
. Принимая в качестве обобщенных сил 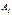 поверхностное натяжение
поверхностное натяжение 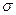 , ЭДС гальванического элемента и т.д. из формулы получаем, что все эти величины при
, ЭДС гальванического элемента и т.д. из формулы получаем, что все эти величины при 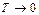 перестают зависеть от температуры и следовательно, температурный коэффициент поверхностного натяжения
перестают зависеть от температуры и следовательно, температурный коэффициент поверхностного натяжения 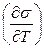 температурный коэффициент ЭДС и т.д. должны обращаться в нуль при приближении температуры к абсолютному нулю. (температурный коэффициент поляризации
температурный коэффициент ЭДС и т.д. должны обращаться в нуль при приближении температуры к абсолютному нулю. (температурный коэффициент поляризации 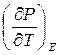 , намагниченности
, намагниченности 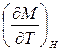 и т.д...). Эти выводы из III начала ТД подтверждаются экспериментально.
и т.д...). Эти выводы из III начала ТД подтверждаются экспериментально.
3) Вычисление энтропии и поведение теплоемкостей при 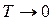 .
.
Третье начало ТД упростило вычисление всех термодинамических функций. До установления третьего начала для вычисления энтропии необходимо было знать температурную зависимость теплоемкости и термическое уравнение состояния.
Согласно третьему началу, энтропию можно находить, зная лишь зависимость теплоемкости от температуры и не располагая термическим уравнением состояния, которое для конденсированных тел неизвестно. Действительно из выражений для теплоемкостей 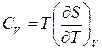 ,
, 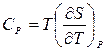 по третьему началу, интегрированием получаем:
по третьему началу, интегрированием получаем: 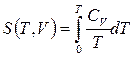 ,
, 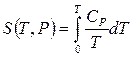
Важнейшая задача вычисления энтропии сводится к определению лишь температурной зависимости теплоемкости. По третьему началу энтропия при 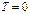 конечна, поэтому интегралы в формулах должны быть сходящимися. Это будет выполняться, если подынтегральные функции
конечна, поэтому интегралы в формулах должны быть сходящимися. Это будет выполняться, если подынтегральные функции 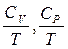 на нижнем пределе возрастают медленнее, чем
на нижнем пределе возрастают медленнее, чем 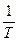 :
:
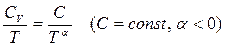 поэтому
поэтому 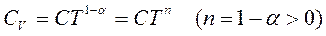 и,следовательно
и,следовательно 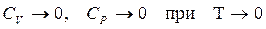
теплоемкости стремятся к нулю быстрее, чем 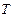 .
.
5 ) Вычисление энтропийной и химической постоянных идеальный газов.
Второе начало ТД оставляет открытым вопрос о явном виде энтропийной и химической постоянных идеального газа. Знание этих постоянных необходимо при рассмотрении равновесия в различных системах (химические реакции, испарение и др.). Третье начало может быть косвенно использовано для решения этой задачи, хотя классический идеальный газ и не удовлетворяет третьему началу.
Идея вычисления состоит в том, что рассматривается условие равновесия газа и твердого тела одного и того же вещества (равенство химических потенциалов вещества в обеих фазах), в которое входят выражения энтропии, как газа, так и твердого тела. Энтропия твердого тела определяется формулами 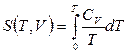 ,
, 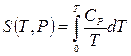 . Для энтропии идеального газа используется выражение
. Для энтропии идеального газа используется выражение 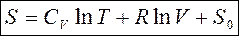 . Энтропийная постоянная
. Энтропийная постоянная 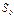 в уравнении связана с химической постоянной газа. Эти постоянные можно вычислить методами статистической физики.
в уравнении связана с химической постоянной газа. Эти постоянные можно вычислить методами статистической физики.
Date: 2015-05-09; view: 1051; Нарушение авторских прав