Атом водорода в квантовой механике. Решение задачи об энергетических уравнениях электрона для атома водорода (а также водородоподобных систем: иона гелия Не+

Решение задачи об энергетических уравнениях электрона для атома водорода (а также водородоподобных систем: иона гелия Не ⁺, двукратно ионизированного лития Li⁺⁺ и др.) сводится к задаче о движении электрона в кулоновском поле ядра.

Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z = 1),

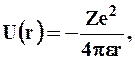
характер закона природы. Уравнение Шредингера имеет вид

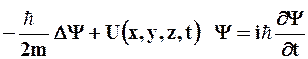, (8.9)

где 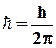; m – массачастицы; 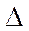- оператор Лапласа

;

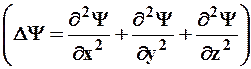i -мнимая единица; U (х, у, z, t) - потенциальная функция частицы в силовом поле, в котором она движется: 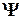(х, у, z, t) - искомая волновая функция частицы.

Уравнение (8.9) справедливо для любой частицы, движущейся с малой скоростью, т.е. со скоростью v<<с, И дополняется условиями, накладываемыми на волновую функцию: 1) конечность, однозначность и непрерывность; 2) производные

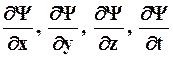
должны быть непрерывны; 3) функция 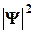должна быть интегрируема: (это условие в простейших случаях сводится к условию нормировки вероятностей).

Уравнение (8.9) является общим уравнением Шредингера или уравнением, зависящим от времени. Для многих Физических явлений, происходящих в микромире, уравнение (8.9) можно упростить, исключив зависимость 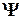от времени. Иными словами, найти уравнение Шредингера для стационарных состояний, т.е. с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется, стационарно, т.е. функция U = U (x,y,z) не зависит явно от времени и имеет смысл потенциальной энергии. В данном случае решение уравнения Шредингера может быть представлено в виде произведения двух функций, одна из которых есть функция только координат, другая - только времени.

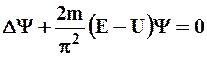. (8.10)

Уравнение (8.10) называется уравнением Шредингера для стационарных состояний.

В это уравнение в качестве параметра входит полная энергия Е частицы. В теории дифференциальных уравнений доказывается, что подобные уравнения имеют бесчисленное множество решений, из которых посредством наложения граничных условий отбирают имеющие физический смысл. Для уравнения Шредингера такими являются условия регулярности волновых функций: конечность, однозначность и непрерывность вместе со своими первыми производными. Таким образом, реальный физический смысл имеют только такие решения, которые выражаются регулярными функциями 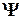. Но регулярные решения имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи. Эти значения энергии называются собственными. Решения же, которые соответствуют собственным значениям энергии, называются собственными функциями. Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном, или сплошном спектре, во втором - о дискретном спектре.

Date: 2015-05-08; view: 593; Нарушение авторских прав